Question

在空間坐標系中，已知直角三角形ABC的三個頂點為A（-3，-2，1）、B（-1，-1，-1）、C（-5，x，0），則x的值為________．

Answer 1

0或9
分析：先利用坐標，求出向量，再分類討論，利用數量積為0，即可求得x的值．
解答：∵A（-3，-2，1）、B（-1，-1，-1）、C（-5，x，0），
∴，，
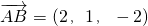
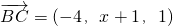
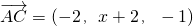
分三種情況：
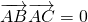
①A為直角，，∴-4+x+2+2=0，∴x=0
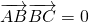
②B為直角，，∴-8+x+1-2=0，∴x=9
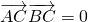
③C為直角，，∴8+（x+1）（x+2）-1=0，x²+3x+9=0，方程無解
綜上，x的值為0或9
故答案為：0或9
點評：本題考查空間向量，考查分類討論的數學思想，解題的關鍵是用坐標表示向量，利用數量積為0建立方程．