
【題目】某學校為了了解學生使用手機的情況,分別在高一和高二兩個年級各隨機抽取了100名學生進行調查.下面是根據調查結果繪制的學生日均使用手機時間的頻數分布表和頻率分布直方圖,將使用手機時間不低于80分鐘的學生稱為“手機迷”.

高一學生日均使用手機時間的頻數分布表
時間分組 | 頻數 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)將頻率視為概率,估計哪個年級的學生是“手機迷”的概率大?請說明理由.
(2)在高二的抽查中,已知隨機抽到的女生共有55名,其中10名為“手機迷”.根據已知條件完成下面的2×2列聯表,并據此資料你有多大的把握認為“手機迷”與性別有關?
非手機迷 | 手機迷 | 合計 | |
男 | |||
女 | |||
合計 |
附:隨機變量 (其中
(其中![]() 為樣本總量).
為樣本總量).
參考數據 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
【答案】(1) 高一年級的學生是“手機迷”的概率大;(2) 有90%的把握認為“手機迷”與性別有關.
【解析】
試題分析:(1)由頻率分布直方圖分別計算高一學生與高二學生手機謎的概率,并比較大小即可;(2)根據頻率分布直方圖求出在抽取的100人中“手機謎”與“非手機謎”中男、女人數,填入列聯表,代入公式計算觀察值![]() ,與參考數據表格對比即可.
,與參考數據表格對比即可.
試題解析: (1)由頻數分布表可知,高一學生是“手機迷”的概率為![]()
由頻率分布直方圖可知,高二學生是“手機迷”的概率為![]() =(0.0025+0.010)×20=0.25
=(0.0025+0.010)×20=0.25
因為P1>P2,所以高一年級的學生是“手機迷”的概率大.
(2)由頻率分布直方圖可知,在抽取的100人中,
“手機迷”有(0.010+0.0025)×20×100=25(人),
非手機迷有100﹣25=75(人).
從而2×2列聯表如下:
非手機迷 | 手機迷 | 合計 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合計 | 75 | 25 | 100 |
將2×2列聯表中的數據代入公式計算,
得![]()
因為3.030>2.706,所以有90%的把握認為“手機迷”與性別有關.


 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】某河上有座拋物線型拱橋,當水面距拱頂5m時水面寬為8m,一木船寬為4m,高為2m,載貨后木船露在水面上的部分高為0.75m,問水面上漲到與拱頂相距多少時,木船開始不能通過。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個盒子里裝有6張卡片,上面分別寫著如下定義域為![]() 的函數:
的函數:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)現在從盒子中任意取兩張卡片,記事件![]() 為“這兩張卡片上函數相加,所得新函數是奇函數”,求事件
為“這兩張卡片上函數相加,所得新函數是奇函數”,求事件![]() 的概率;
的概率;
(2)從盒中不放回逐一抽取卡片,若取到一張卡片上的函數是偶函數則停止抽取,否則繼續進行,記停止時抽取次數為![]() ,寫出
,寫出![]() 的分布列,并求其數學期望
的分布列,并求其數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若<<0,則下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正確的是( )
(A)①④ (B)②③ (C)①③ (D)②④
查看答案和解析>>
科目:高中數學 來源: 題型:
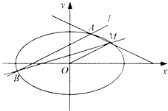
【題目】如圖,橢圓![]() :
:![]() (
(![]() )的短軸長為
)的短軸長為![]() ,點
,點![]() 在C上,平行于OM的直線
在C上,平行于OM的直線![]() 交橢圓C于不同的兩點A,B.
交橢圓C于不同的兩點A,B.
(1)求橢圓![]() 的方程;
的方程;
(2)證明:直線MA,MB與![]() 軸總圍成等腰三角形.
軸總圍成等腰三角形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連江一中第49屆田徑運動會提出了“我運動、我陽光、我健康、我快樂”的口號,某同學要設計一張如圖所示的豎向張貼的長方形海報進行宣傳,要求版心面積為162 ![]() (版心是指圖中的長方形陰影部分,
(版心是指圖中的長方形陰影部分,![]() 為長度單位分米),上、下兩邊各空2
為長度單位分米),上、下兩邊各空2 ![]() ,左、右兩邊各空1
,左、右兩邊各空1 ![]() .
.

(1)若設版心的高為![]()
![]() ,求海報四周空白面積關于
,求海報四周空白面積關于![]() 的函數
的函數![]() 的解析式;
的解析式;
(2)要使海報四周空白面積最小,版心的高和寬該如何設計?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com