(Ⅰ)證明:∵x∈R,f(-x)=a
-x+a
x=a
x+a
-x=f(x)…(3分)
∴函數f ( x )是偶函數,∴函數f ( x )的圖象關于y軸對稱…(4分)
(Ⅱ)證明:設0<x
1<x
2,則f(x
1)-f(x
2)=
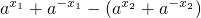
(1)當a>1時,
由0<x
1<x
2,則x
1+x
2>0,則

、
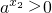
、

、
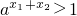
∴f(x
1)-f(x
2)<0,∴f(x
1)<f(x
2);
(2)當0<a<1時,
由0<x
1<x
2,則x
1+x
2>0,則

、
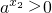
、

、

;
∴f(x
1)-f(x
2)<0,∴f(x
1)<f(x
2);
所以,對于任意a(a>0且a≠1),f(x)在(0,+∞)上都為增函數.
(Ⅲ)由(Ⅱ)知f(x)在(0,+∞)上為增函數,則當x∈[1,2]時,函數f (x )亦為增函數;
由于函數f(x)的最大值為

,則f(2)=

即
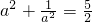
,解得

,或
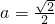
(Ⅳ)由(Ⅰ)(Ⅱ)證知f(x) 是偶函數且在(0,+∞)上為增函數,則知f(x)在(-∞,0)上為減函數;
則當x∈[-2,-1]時,函數f (x )為減函數
由于函數f(x)的最大值為

,則f(-2)=

即

,解得

,或
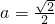
分析:(Ⅰ)要證明函數f ( x )的圖象關于y軸對稱則只須證明函數f ( x )是偶函數;
(Ⅱ)對底數分類討論,利用單調性的證題步驟加以證明;
(Ⅲ)當x∈[1,2]時,函數f (x )為增函數,利用函數f (x )的最大值為

,建立方程,可求a的值;
(Ⅳ)由(Ⅰ)(Ⅱ)證知f(x) 是偶函數且在(0,+∞)上為增函數,則知f(x)在(-∞,0)上為減函數;
則當x∈[-2,-1]時,函數f (x )為減函數,利用函數f (x )的最大值為

,建立方程,可求a的值.
點評:本題考查函數的奇偶性,考查函數的單調性,考查函數的最值,解題的關鍵是靈活運用函數的單調性與奇偶性,屬于中檔題.

 ,求此時a的值.
,求此時a的值. ,求此時a的值.
,求此時a的值.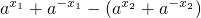
 、
、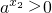 、
、 、
、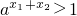
 、
、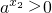 、
、 、
、 ;
; ,則f(2)=
,則f(2)=
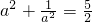 ,解得
,解得 ,或
,或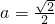
 ,則f(-2)=
,則f(-2)=
 ,解得
,解得 ,或
,或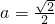
 ,建立方程,可求a的值;
,建立方程,可求a的值; ,建立方程,可求a的值.
,建立方程,可求a的值.
