
【題目】購買一輛某品牌新能源汽車,在行駛三年后,政府將給予適當金額的購車補貼.某調研機構對擬購買該品牌汽車的消費者,就購車補貼金額的心理預期值進行了抽樣調查,其樣本頻率分布直方圖如圖所示
.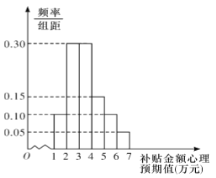
(1)估計擬購買該品牌汽車的消費群體對購車補貼金額的心理預期值的方差(同一組中的數據用該組區間的中點值作代表);
(2)將頻率視為概率,從擬購買該品牌汽車的消費群體中隨機抽取![]() 人,記對購車補貼金額的心理預期值高于
人,記對購車補貼金額的心理預期值高于![]() 萬元的人數為
萬元的人數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)統計最近![]() 個月該品牌汽車的市場銷售量,得其頻數分布表如下:
個月該品牌汽車的市場銷售量,得其頻數分布表如下:
月份 |
|
|
|
|
|
銷售量(萬輛) |
|
|
|
|
|
試預計該品牌汽車在![]() 年
年![]() 月份的銷售量約為多少萬輛?
月份的銷售量約為多少萬輛?
附:對于一組樣本數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
【答案】(1)1.7;(2)![]() ,見解析;(2)2.
,見解析;(2)2.
【解析】
(1)平均數的估計值為每個小矩形組中值乘以小矩形面積的和;
(2)易得![]() ,由二項分布列的期望公式計算;
,由二項分布列的期望公式計算;
(3)利用所給公式計算出回歸直線![]() 即可解決.
即可解決.
(1)由頻率分布直方圖可知,消費群體對購車補貼金額的心理預期值的平均數的估計值為
![]() ,所以方差的估計
,所以方差的估計
值為![]()
![]()
![]()
![]()
![]()
![]() ;
;
(2)由頻率分布直方圖可知,消費群體對購車補貼金額的心理預期值高于3萬元的
頻率為![]() ,則
,則![]() ,所以
,所以![]() 的分布列為
的分布列為
![]() ,數學期望
,數學期望![]() ;
;
(3)將 2018年11月至2019年3月的月份數依次編號為 1,2,3,4,5,
記 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,由 散 點 圖可知,
,由 散 點 圖可知,
5組樣本數據呈線性相關關系,因為![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,則
,則![]() ,
,![]() ,
,
所以回歸直線方程為![]() ,當
,當![]() 時,
時,![]() ,預計該品
,預計該品
牌汽車在![]() 年
年![]() 月份的銷售量約為2萬輛.
月份的銷售量約為2萬輛.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x﹣a|,a∈R.
(1)當f(2)+f(﹣2)>4時,求a的取值范圍;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函數
.已知函數![]() ,
,![]() .
.
(1)設![]() ,求函數
,求函數![]() 在
在![]() 上零點的個數;
上零點的個數;
(2)試探討是否存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)既是二次函數又是冪函數,函數g(x)是R上的奇函數,函數![]() =
=![]() +1,則h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
+1,則h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(﹣1)+…h(﹣2016)+h(﹣2017)+h(﹣2018)=___________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元五世紀,數學家祖沖之估計圓周率![]() 的值的范圍是:3.1415926<
的值的范圍是:3.1415926<![]() <3.1415927,為紀念祖沖之在圓周率的成就,把3.1415926稱為“祖率”,這是中國數學的偉大成就.某小學教師為幫助同學們了解“祖率”,讓同學們把小數點后的7位數字1,4,1,5,9,2,6進行隨機排列,整數部分3不變,那么可以得到大于3.14的不同數字有( )
<3.1415927,為紀念祖沖之在圓周率的成就,把3.1415926稱為“祖率”,這是中國數學的偉大成就.某小學教師為幫助同學們了解“祖率”,讓同學們把小數點后的7位數字1,4,1,5,9,2,6進行隨機排列,整數部分3不變,那么可以得到大于3.14的不同數字有( )
A.2280B.2120C.1440D.720
查看答案和解析>>
科目:高中數學 來源: 題型:
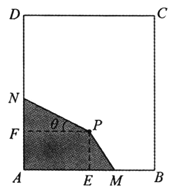
【題目】(題文)如圖,長方形材料![]() 中,已知
中,已知![]() ,
,![]() .點
.點![]() 為材料
為材料![]() 內部一點,
內部一點,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 現要在長方形材料
. 現要在長方形材料![]() 中裁剪出四邊形材料
中裁剪出四邊形材料![]() ,滿足
,滿足![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() ,
,![]() 上.
上.
(1)設![]() ,試將四邊形材料
,試將四邊形材料![]() 的面積表示為
的面積表示為![]() 的函數,并指明
的函數,并指明![]() 的取值范圍;
的取值范圍;
(2)試確定點![]() 在
在![]() 上的位置,使得四邊形材料
上的位置,使得四邊形材料![]() 的面積
的面積![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“克拉茨猜想”又稱“![]() 猜想”,是德國數學家洛薩·克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數
猜想”,是德國數學家洛薩·克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半;如果
是偶數,就將它減半;如果![]() 是奇數,就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.已知正整數
是奇數,就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.已知正整數![]() 經過7次運算后首次得到1,則
經過7次運算后首次得到1,則![]() 的所有不同取值的集合為____________.
的所有不同取值的集合為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com