
【題目】某大型娛樂場有兩種型號的水上摩托,管理人員為了了解水上摩托的使用及給娛樂城帶來的經濟收入情況,對該場所最近6年水上摩托的使用情況進行了統計,得到相關數據如表:
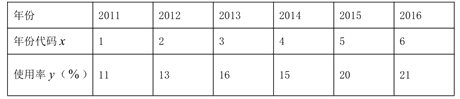
(1)請根據以上數據,用最小二乘法求水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程,并預測該娛樂場2018年水上摩托的使用率;
的線性回歸方程,并預測該娛樂場2018年水上摩托的使用率;
(2)隨著生活水平的提高,外出旅游的老百姓越來越多,該娛樂場根據自身的發展需要,準備重新購進一批水上摩托,其型號主要是目前使用的Ⅰ型、Ⅱ型兩種,每輛價格分別為1萬元、1.2萬元.根據以往經驗,每輛水上摩托的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:

已知每輛水上摩托從購入到淘汰平均年收益是0.8萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤=收益-購車成本)的期望值為參考值,則該娛樂場的負責人應該選購Ⅰ型水上摩托還是Ⅱ型水上摩托?
附:回歸直線方程為![]() ,其中
,其中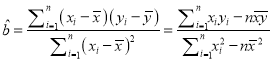 ,
, ![]() .參考數據
.參考數據![]() ,
, ![]()
【答案】(1)25%(2)應該選購Ⅱ型水上摩托.
【解析】試題分析:(1)根據所給數據求出回歸方程,利用回歸方程預測![]() ,即 2018年水上摩托的使用率;(2))分別由頻率估計概率,結合直方圖可知水上摩托每輛可使用1年、2年、3年和4年的概率,計算Ⅰ型和Ⅱ型摩托純利潤的期望,比較大小即可得出結論.
,即 2018年水上摩托的使用率;(2))分別由頻率估計概率,結合直方圖可知水上摩托每輛可使用1年、2年、3年和4年的概率,計算Ⅰ型和Ⅱ型摩托純利潤的期望,比較大小即可得出結論.
試題解析:
(1)由表格數據可得![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴ ,
,
∴![]() ,
,
∴水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程為
的線性回歸方程為![]() .
.
當![]() 時,
時, ![]() ,
,
故預測該娛樂場2018年水上摩托的使用率為25%.
(2)由頻率估計概率,結合條形圖知Ⅰ型水上摩托每輛可使用1年、2年、3年和4年的概率分別為0.2,0.3,0.3,0.2,
∴每輛Ⅰ型水上摩托可產生的純利潤期望值
![]()
![]() (萬元).
(萬元).
由頻率估計概率,結合條形圖知Ⅱ型水上摩托每輛可使用1年、2年、3年和4年的概率分別為0.1,0.2,0.4和0.3,
∴每輛Ⅱ型水上摩托可產生的純利潤期望值
![]()
![]() (萬元).
(萬元).
∵![]() .
.
∴應該選購Ⅱ型水上摩托.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】(導學號:05856325)已知函數f(x)=![]() +eln x,直線l:y=kx(k≠0)與函數f(x)的圖象相切于點A(t,f(t))(f(t)≠0),則( )
+eln x,直線l:y=kx(k≠0)與函數f(x)的圖象相切于點A(t,f(t))(f(t)≠0),則( )
A. t∈(0,1) B. t∈(1,e) C. t∈(e,3) D. t∈(3,e2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+φ) ![]() 在某一個周期內的圖象時,列表并填入了部分數據,如下表:
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | -5 | 0 |
(1)請將上表數據補充完整,并直接寫出函數f(x)的解析式;
(2)將y=f(x)圖象上所有點向左平行移動θ(θ>0)個單位長度,得到y=g(x)的圖象.若y=g(x)圖象的一個對稱中心為![]() ,求θ的最小值.
,求θ的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名同學準備參加考試,在正式考試之前進行了十次模擬測試,測試成績如下:
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)畫出甲、乙兩人成績的莖葉圖,求出甲同學成績的平均數和方差,并根據莖葉圖,寫出甲、乙兩位同學平均成績以及兩位同學成績的中位數的大小關系的結論;
(2)規定成績超過127為“良好”,現在老師分別從甲、乙兩人成績中各隨機選出一個,求選出成績“良好”的個數![]() 的分布列和數學期望.
的分布列和數學期望.
(注:方差![]() ,其中
,其中![]() 為
為![]() 的平均數)
的平均數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
, ![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的極坐標方程化為直角坐標方程,并說明曲線
的極坐標方程化為直角坐標方程,并說明曲線![]() 的形狀;
的形狀;
(2)若直線![]() 經過點
經過點![]() ,求直線
,求直線![]() 被曲線
被曲線![]() 截得的線段的長.
截得的線段的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱ABC-A1B1C1的各棱長都等于2,D在AC1上,F為BB1的中點,且FD⊥AC1,有下述結論:
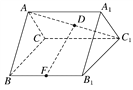
①AC1⊥BC;
②![]() =1;
=1;
③平面FAC1⊥平面ACC1A1;
④三棱錐D-ACF的體積為![]() .
.
其中正確結論的個數為( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題12分)如圖,在海岸線![]() 一側有一休閑游樂場,游樂場的前一部分邊界為曲線段
一側有一休閑游樂場,游樂場的前一部分邊界為曲線段![]() ,該曲線段是函數
,該曲線段是函數![]() ,
,![]() 的圖像,圖像的最高點為
的圖像,圖像的最高點為![]() .邊界的中間部分為長
.邊界的中間部分為長![]() 千米的直線段
千米的直線段![]() ,且
,且![]() .游樂場的后一部分邊界是以
.游樂場的后一部分邊界是以![]() 為圓心的一段圓弧
為圓心的一段圓弧![]() .
.

(1)求曲線段![]() 的函數表達式;
的函數表達式;
(2)曲線段![]() 上的入口
上的入口![]() 距海岸線
距海岸線![]() 最近距離為
最近距離為![]() 千米,現準備從入口
千米,現準備從入口![]() 修一條筆直的景觀路到
修一條筆直的景觀路到![]() ,求景觀路
,求景觀路![]() 長;
長;
(3)如圖,在扇形![]() 區域內建一個平行四邊形休閑區
區域內建一個平行四邊形休閑區![]() ,平行四邊形的一邊在海岸線
,平行四邊形的一邊在海岸線![]() 上,一邊在半徑
上,一邊在半徑![]() 上,另外一個頂點
上,另外一個頂點![]() 在圓弧
在圓弧![]() 上,且
上,且![]() ,求平行四邊形休閑區
,求平行四邊形休閑區![]() 面積的最大值及此時
面積的最大值及此時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com