
分析 (1)由題意可得c=2,即可求出b=2,即可求出橢圓的標準方程,
(2)設A(2$\sqrt{2}$cosα,2sinα),B(2$\sqrt{2}$cosβ,2sinβ),根據題意和點P在橢圓上,化簡整理可得a-β=$\frac{π}{2}$,再根據中點坐標公式,消α,線段AB中點Q的軌跡為E的方程為$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1,再設M,N兩點的坐標為(x1,y1),(x2,y2),根據弦長公式即可求出.
解答 解:(1)∵點F1,F2與橢圓短軸的一個端點構成斜邊長為4的直角三角形.
∴2c=4,b=2,
故c=2,a=2$\sqrt{2}$,
故橢圓C的標準方程為:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)設A(2$\sqrt{2}$cosα,2sinα),B(2$\sqrt{2}$cosβ,2sinβ),
∵$\overrightarrow{OP}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{4}{5}$$\overrightarrow{OB}$,
∴$\overrightarrow{OP}$=($\frac{6\sqrt{2}cosα+8\sqrt{2}cosβ}{5}$,$\frac{6sinα+8sinβ}{5}$),
∵點P在橢圓上,
∴(3cosα+4cosβ)2+(3sinα+4sinβ)2=25,
∴cosαcosβ+sinαsinβ=0,
∴cos(α-β)=0,
∴a-β=$\frac{π}{2}$,
∴B(2$\sqrt{2}$sinα,-2cosα),
∴AB中點Q的坐標為($\sqrt{2}$cosα+$\sqrt{2}$sinα,sinα-cosα),
設Q的點坐標為(x,y),
∴x=$\sqrt{2}$cosα+$\sqrt{2}$sinα,y=sinα-cosα,
∴$\frac{{x}^{2}}{4}$=cos2α+2cosαsinα+sin2α=1+2cosαsinα,y2=cos2α-2cosαsinα+sin2α=1-2cosαsinα
∴$\frac{{x}^{2}}{4}$+y2=2,
即線段AB中點Q的軌跡為E的方程為$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1,
設M,N兩點的坐標為(x1,y1),(x2,y2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\\{y=x+1}\end{array}\right.$,消y,整理得5x2+8x-4=0,
∴x1+x2=-$\frac{8}{5}$,x1x2=-$\frac{4}{5}$,
∴|MN|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{\frac{64}{25}+\frac{16}{5}}$=$\frac{12\sqrt{2}}{5}$.
點評 本題考查了橢圓的方程,弦長公式,以及點的軌跡方程,關鍵是巧設點的坐標,屬于難題.


科目:高中數學 來源: 題型:選擇題
| A. | y=-2x+3 | B. | y=x | C. | y=3x-2 | D. | y=2x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
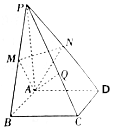 如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分別為PB,PD的中點.
如圖,在四棱錐P-ABCD中,底面是邊長為2$\sqrt{3}$的菱形,且∠ABC=60°,PA⊥平面ABCD,PA=2$\sqrt{6}$,M,N分別為PB,PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
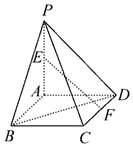 如圖,平面PAD⊥平面ABCD,四邊形ABCD為正方形,∠PAD=90°,且PA=AD=2,E,F分別是線段PA,CD的中點,則異面直線EF與BD所成角的余弦值為$\frac{\sqrt{3}}{6}$.
如圖,平面PAD⊥平面ABCD,四邊形ABCD為正方形,∠PAD=90°,且PA=AD=2,E,F分別是線段PA,CD的中點,則異面直線EF與BD所成角的余弦值為$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
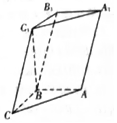 如圖所示,三棱柱ABC-A1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.
如圖所示,三棱柱ABC-A1B1C1中,已知AB⊥側面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com