
【題目】某市高中某學(xué)科競賽中,某區(qū)![]() 名考生的參賽成績的頻率分布直方圖如圖所示.
名考生的參賽成績的頻率分布直方圖如圖所示.
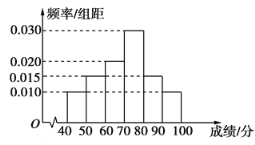
(1)求這![]() 名考生的平均成績
名考生的平均成績![]() (同一組中數(shù)據(jù)用該組區(qū)間中點值作代表);
(同一組中數(shù)據(jù)用該組區(qū)間中點值作代表);
(2)記![]() 分以上為合格,
分以上為合格,![]() 分及以下為不合格,結(jié)合頻率分布直方圖完成下表,能否在犯錯誤概率不超過
分及以下為不合格,結(jié)合頻率分布直方圖完成下表,能否在犯錯誤概率不超過![]() 的前提下認為該學(xué)科競賽成績與性別有關(guān)?
的前提下認為該學(xué)科競賽成績與性別有關(guān)?
不合格 | 合格 | 合計 | |
男生 |
| ||
女生 |
| ||
合計 |
|
附:
|
|
|
|
|
|
|
|
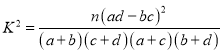 .
.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
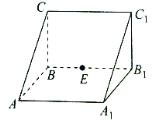
【題目】如圖,三棱柱![]() 中,側(cè)棱
中,側(cè)棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,外接球的球心為
,外接球的球心為![]() ,點
,點![]() 是側(cè)棱
是側(cè)棱![]() 上的一個動點.有下列判斷:①直線
上的一個動點.有下列判斷:①直線![]() 與直線
與直線![]() 是異面直線;②
是異面直線;②![]() 一定不垂直于
一定不垂直于![]() ; ③三棱錐
; ③三棱錐![]() 的體積為定值;④
的體積為定值;④![]() 的最小值為
的最小值為![]() .其中正確的序號是______.
.其中正確的序號是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,將
的中點,將![]() 沿
沿![]() 折起得到圖(二),點
折起得到圖(二),點![]() 為棱
為棱![]() 上的動點.
上的動點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 為
為![]() ,點
,點![]() 為
為![]() 中點,求二面角
中點,求二面角![]() 余弦值的平方.
余弦值的平方.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】 山東省《體育高考方案》于2012年2月份公布,方案要求以學(xué)校為單位進行體育測試,某校對高三1班同學(xué)按照高考測試項目按百分制進行了預(yù)備測試,并對50分以上的成績進行統(tǒng)計,其頻率分布直方圖如圖所示,若90~100分數(shù)段的人數(shù)為2人.
(Ⅰ)請估計一下這組數(shù)據(jù)的平均數(shù)M;
(Ⅱ)現(xiàn)根據(jù)初賽成績從第一組和第五組(從低分段到高分段依次為第一組、第二組、…、第五組)中任意選出兩人,形成一個小組.若選出的兩人成績差大于20,則稱這兩人為“幫扶組”,試求選出的兩人為“幫扶組”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
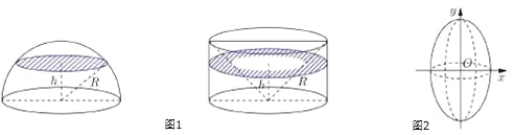
【題目】(數(shù)學(xué)文卷·2017屆重慶十一中高三12月月考第16題) 現(xiàn)介紹祖暅原理求球體體積公式的做法:可構(gòu)造一個底面半徑和高都與球半徑相等的圓柱,然后在圓柱內(nèi)挖去一個以圓柱下底面圓心為頂點,圓柱上底面為底面的圓錐,用這樣一個幾何體與半球應(yīng)用祖暅原理(圖1),即可求得球的體積公式.請研究和理解球的體積公式求法的基礎(chǔ)上,解答以下問題:已知橢圓的標準方程為![]() ,將此橢圓繞y軸旋轉(zhuǎn)一周后,得一橄欖狀的幾何體(圖2),其體積等于______.
,將此橢圓繞y軸旋轉(zhuǎn)一周后,得一橄欖狀的幾何體(圖2),其體積等于______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了解人們對“延遲退休年齡政策”的態(tài)度,某部門從年齡在15歲到65歲的人群中隨機調(diào)查了100人,并得到如圖所示的頻率分布直方圖,在這100人中不支持“延遲退休年齡政策”的人數(shù)與年齡的統(tǒng)計結(jié)果如表所示:


(1)由頻率分布直方圖,估計這100人年齡的平均數(shù);
(2)根據(jù)以上統(tǒng)計數(shù)據(jù)填寫下面的2![]() 2列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過5%的前提下,認為以45歲為分界點的不同人群對“延遲退休年齡政策”的態(tài)度存在差異?
2列聯(lián)表,據(jù)此表,能否在犯錯誤的概率不超過5%的前提下,認為以45歲為分界點的不同人群對“延遲退休年齡政策”的態(tài)度存在差異?
45歲以下 | 45歲以上 | 總計 | |
不支持 | |||
支持 | |||
總計 |
參考數(shù)據(jù):
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(Ⅰ)求實數(shù)![]() 的值;
的值;
(Ⅱ)設(shè)![]() .
.
(i)若函數(shù)![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大值;
的最大值;
(ii)當![]() 時,判斷函數(shù)
時,判斷函數(shù)![]() 有幾個零點,并給出證明.
有幾個零點,并給出證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是平面內(nèi)共始點的三個非零向量,且兩兩不共線,
是平面內(nèi)共始點的三個非零向量,且兩兩不共線,![]() 有下列命題:
有下列命題:
(1)關(guān)于![]() 的方程
的方程![]() 可能有兩個不同的實數(shù)解;
可能有兩個不同的實數(shù)解;
(2)關(guān)于![]() 的方程
的方程![]() 至少有一個實數(shù)解;
至少有一個實數(shù)解;
(3)關(guān)于![]() 的方程
的方程![]() 最多有一個實數(shù)解;
最多有一個實數(shù)解;
(4)關(guān)于![]() 的方程
的方程![]() 若有實數(shù)解,則三個向量的終點不可能共線;
若有實數(shù)解,則三個向量的終點不可能共線;
上述命題正確的序號是__________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù)),
為自然對數(shù)的底數(shù)),![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的極小值;
的極小值;
(2)若當![]() 時,關(guān)于
時,關(guān)于![]() 的方程
的方程![]() 有且只有一個實數(shù)解,求
有且只有一個實數(shù)解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com