
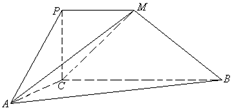
 如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.| NH |
| MH |
| ||
| 7 |
|
| n |
| CP |
| n |
| CP |
| ||||
|
|
| ||||
|
|
| AC2+CN2-2AC•CN•cos120° |
| 3 |
| 3 |
| ||
| 2 |
| MN2+NH2 |
| ||
| 2 |
| NH |
| MH |
| ||
| 7 |
| ||
| 7 |
| MN•NH |
| MH |
| ||
| 7 |
2
| ||
| 7 |

| CP |
| AM |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| AM |
| CP |
| ||||
|
|
| z2 | ||
|
| z | ||
|
| 1 |
| 2 |
| AM |
| ||
| 2 |
| 3 |
| 2 |
| n |
|
|
|
| n |
| ||
| 3 |
| CP |
| n |
| CP |
| ||||
|
|
| ||
| 7 |
| ||
| 7 |
| ||||
|
|
2
| ||
| 7 |


科目:高中數學 來源: 題型:
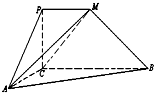 如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北衡水中學高三上學期期中考試理科數學試卷(解析版) 題型:解答題
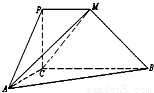
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
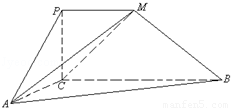
(1)求證:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求點B到平面MAC的距離.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年重慶市三峽聯盟高三3月聯考理科數學試卷(解析版) 題型:解答題
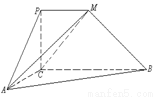
如圖,四邊形PCBM是直角梯形,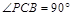 ,
,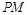 ∥
∥ ,
,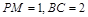 .又
.又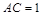 ,
, ,直線AM與直線PC所成的角為
,直線AM與直線PC所成的角為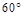 .
.
(1)求證: ;
;
(2)求二面角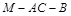 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源:2013年江西省南昌三中高考數學三模試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com