
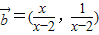 ,
,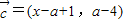 ,解關于x的不等式
,解關于x的不等式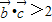 (其中a>1)
(其中a>1)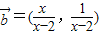 ,
,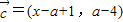 ,根據平面向量的數量積公式,我們易求出
,根據平面向量的數量積公式,我們易求出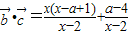 ,進而可將不等式
,進而可將不等式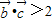 轉化為(x-a)(x-1)(x-2)>0,由a>1,我們分1<a<2,a=2和a>2三種情況分別求出不等式的解集,即可得到答案.
轉化為(x-a)(x-1)(x-2)>0,由a>1,我們分1<a<2,a=2和a>2三種情況分別求出不等式的解集,即可得到答案.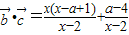 ,(2分)
,(2分)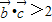 ,得
,得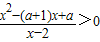
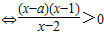 (4分)
(4分)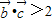 轉化為(x-a)(x-1)(x-2)>0是解答本題的關鍵.
轉化為(x-a)(x-1)(x-2)>0是解答本題的關鍵. 

 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com