
 ,且b<0,試判斷函數F(x)的單調性;
,且b<0,試判斷函數F(x)的單調性;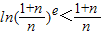 恒成立.
恒成立.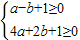 ,然后利用線性規劃,求出目標函數z=3a-b的取值范圍;
,然后利用線性規劃,求出目標函數z=3a-b的取值范圍;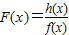 ,且b<0,我們可以分別求出函數F(x)的解析式及其導函數的解析式,然后利用導數學判斷出函數F(x)的單調性;
,且b<0,我們可以分別求出函數F(x)的解析式及其導函數的解析式,然后利用導數學判斷出函數F(x)的單調性;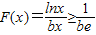 ,即
,即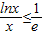 ,進而根據對數的運算性質證得答案.
,進而根據對數的運算性質證得答案. ,x∈(0,+∞),利用導數法,可以證得p(x)在(0,e]上單調遞增,在[e,+∞)上單調遞減,即對任意的x∈(0,+∞)恒有
,x∈(0,+∞),利用導數法,可以證得p(x)在(0,e]上單調遞增,在[e,+∞)上單調遞減,即對任意的x∈(0,+∞)恒有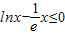 ,即
,即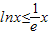 進而根據對數的運算性質證得答案.
進而根據對數的運算性質證得答案.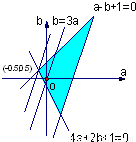 解:(1)解法1:不等式f(x)+g(x)≥0即ax2+bx+1≥0
解:(1)解法1:不等式f(x)+g(x)≥0即ax2+bx+1≥0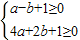 ----------------(2分)
----------------(2分)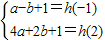 得
得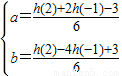 -------------------------(2分)
-------------------------(2分)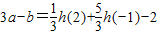
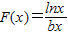 ∴
∴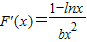 -----------------------------------(6分)
-----------------------------------(6分)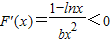 ,當x>e時F'(x)>0
,當x>e時F'(x)>0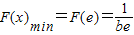
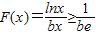 ,------------------------------------------------(11分)
,------------------------------------------------(11分)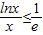 當且僅當x=e時“=”成立
當且僅當x=e時“=”成立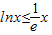 --------------------------------------------------(12分)
--------------------------------------------------(12分)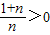 且
且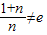 ∴
∴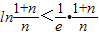
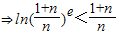
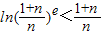 恒成立.-----------------------------------------(14分)
恒成立.-----------------------------------------(14分)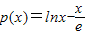 ,x∈(0,+∞)----------------------------------------(10分)
,x∈(0,+∞)----------------------------------------(10分)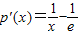 =0得x=e
=0得x=e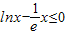 ,即
,即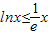
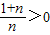 且
且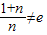 ∴
∴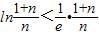

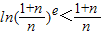 恒成立.-----------------------------------------(14分)
恒成立.-----------------------------------------(14分)

 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:高中數學 來源: 題型:
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 6 |
| 1 |
| 24 |
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| x | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| a |
| 1 |
| b |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com