
(1) 在直角坐標系xOy中,曲線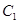 的參數方程為
的參數方程為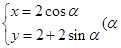 為參數),M為
為參數),M為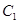 上的動點,P點滿足
上的動點,P點滿足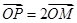 ,點P的軌跡為曲線
,點P的軌跡為曲線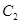 .已知在以O為極點,x軸的正半軸為極軸的極坐標系中,射線
.已知在以O為極點,x軸的正半軸為極軸的極坐標系中,射線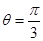 與
與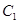 的異于極點的交點為A,與
的異于極點的交點為A,與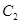 的異于極點的交點為B,求|AB|.
的異于極點的交點為B,求|AB|.
(2) 某旅游景點給游人準備了這樣一個游戲,他制作了“迷尼游戲板”:在一塊傾斜放置的矩形膠合板上釘著一個形如“等腰三角形”的八行鐵釘,釘子之間留有空隙作為通道,自上而下第1行2個鐵釘之間有1個空隙,第2行3個鐵釘之間有2個空隙,…,第8行9個鐵釘之間有8個空隙(如圖所示).東方莊家的游戲規則是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付給莊家2元.若小球到達①②③④號球槽,分別獎4元、2元、0元、-2元.(一個玻璃球的滾動方式:通過第1行的空隙向下滾動,小球碰到第二行居中的鐵釘后以相等的概率滾入第2行的左空隙或右空隙.以后小球按類似方式繼續往下滾動,落入第8行的某一個空隙后,最后掉入迷尼板下方的相應球槽內).恰逢周末,某同學看了一個小時,留心數了數,有80人次玩.試用你學過的知識分析,這一小時內游戲莊家是贏是賠? 通過計算,你得到什么啟示?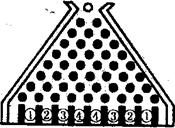
(1)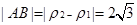 .
.
(2)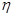 ~B(7,
~B(7, ). 一小時內有80人次玩.游戲莊家通常獲純利為(2+
). 一小時內有80人次玩.游戲莊家通常獲純利為(2+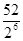 ×)80=225(元)
×)80=225(元)
答:莊家當然是贏家!我們應當學會以所學過的知識為武器,勸說人們不要被這類騙子的騙術所迷惑. 16分
解析試題分析:設P(x,y),則由條件知M(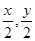 ).由于M點在C1上,所以
).由于M點在C1上,所以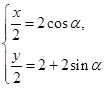 即
即 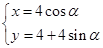
從而 的參數方程為
的參數方程為 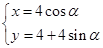 (
(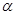 為參數) 4分
為參數) 4分
∴ 曲線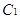 的極坐標方程為
的極坐標方程為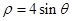 ,曲線
,曲線 的極坐標方程為
的極坐標方程為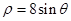 .
.
射線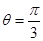 與
與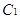 的交點
的交點 的極徑為
的極徑為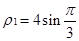 ,
,
射線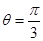 與
與 的交點
的交點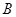 的極徑為
的極徑為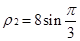 .
.
所以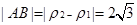 . 8分
. 8分
(2) 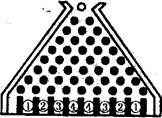
解:游人每玩一次,設游戲莊家獲利為隨機變量 (元);游人每放一球,小球落入球槽,相當于做7次獨立重復試驗,設這個小球落入鐵釘空隙從左到右的次序為隨機變量+1,
(元);游人每放一球,小球落入球槽,相當于做7次獨立重復試驗,設這個小球落入鐵釘空隙從左到右的次序為隨機變量+1,
則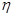 ~B(7,
~B(7, ). 10分
). 10分
因為P( =-4)=P(
=-4)=P(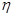 =0或
=0或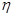 =7)=P(
=7)=P(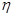 =0)+P(
=0)+P(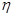 =7)=
=7)=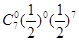 +
+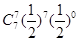 =
=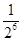
P( =-2)=P(
=-2)=P(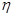 =1或
=1或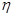 =6)=P(
=6)=P(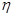 =1)+P(
=1)+P(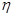 =6)=
=6)= +
+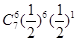 =
=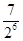
P( =0)=P(
=0)=P(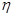 =2或
=2或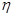 =5)=P(
=5)=P(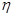 =2)+P(
=2)+P(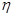 =5)=
=5)= +
+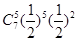 =
=
P( =2)=P(
=2)=P(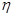 =3或
=3或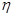 =4)=P(
=4)=P(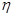 =3)+P(
=3)+P(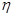 =4)=
=4)=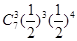 +
+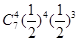 =
=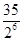
2+E =2+(-4)×
=2+(-4)×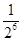 +(-2)×
+(-2)×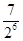 +0×
+0× +2×
+2×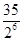 =2+
=2+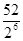 , 14分
, 14分
一小時內有80人次玩.游戲莊家通常獲純利為(2+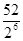 ×)80=225(元)
×)80=225(元)
答:莊家當然是贏家!我們應當學會以所學過的知識為武器,勸說人們不要被這類騙子的騙術所迷惑. 16分
考點:本題主要考查簡單曲線的參數方程、極坐標方程,獨立重復試驗概率計算,隨機變量的分布列及數學期望。
點評:綜合題,本題綜合考查簡單曲線的參數方程、極坐標方程,獨立重復試驗概率計算,隨機變量的分布列及數學期望。(2)作為應用問題,寓教于樂,令人生趣。對計算能力要求較高。


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源: 題型:解答題
在直角坐標平面內,以坐標原點 為極點,
為極點, 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點 的極坐標為
的極坐標為 ,曲線
,曲線 的參數方程為
的參數方程為 (
( 為參數).
為參數).
(1)求直線 的直角坐標方程;
的直角坐標方程;
(2)求點 到曲線
到曲線 上的點的距離的最小值.
上的點的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知直線 的極坐標方程是
的極坐標方程是 .以極點為平面直角坐標系的原點,極軸為
.以極點為平面直角坐標系的原點,極軸為 軸的正半軸,建立平面直角坐標系,在曲線
軸的正半軸,建立平面直角坐標系,在曲線 上求一點,使它到直線
上求一點,使它到直線 的距離最小,并求出該點坐標和最小距離
的距離最小,并求出該點坐標和最小距離
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
曲線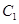 的參數方程為
的參數方程為 (
( 為參數),將曲線
為參數),將曲線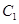 上所有點的橫坐標伸長為原來的2倍,縱坐標伸長為原來的
上所有點的橫坐標伸長為原來的2倍,縱坐標伸長為原來的 倍,得到曲線
倍,得到曲線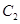 .
.
(Ⅰ)求曲線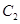 的普通方程;
的普通方程;
(Ⅱ)已知點 ,曲線
,曲線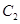 與
與 軸負半軸交于點
軸負半軸交于點 ,
, 為曲線
為曲線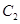 上任意一點, 求
上任意一點, 求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在平面直角坐標系xOy中,已知曲線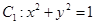 ,將
,將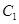 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的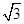 、2倍后得到曲線
、2倍后得到曲線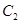 . 以平面直角坐標系xOy的原點O為極點,x軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
. 以平面直角坐標系xOy的原點O為極點,x軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線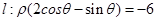 .
.
(1)試寫出直線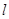 的直角坐標方程和曲線
的直角坐標方程和曲線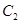 的參數方程;
的參數方程;
(2)在曲線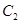 上求一點P,使點P到直線
上求一點P,使點P到直線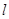 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知曲線C1的極坐標方程為 ,曲線C2的極坐標方程為
,曲線C2的極坐標方程為 ,曲線C1,C2相交于A,B兩點
,曲線C1,C2相交于A,B兩點
(I)把曲線C1,C2的極坐標方程轉化為直角坐標方程;
(II)求弦AB的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分10分)選修4—4:坐標系與參數方程選講
在直角坐標系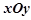 中,直線l的參數方程為:
中,直線l的參數方程為: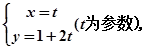 在以O為極點,以x 軸的正半軸為極軸的極坐標系中,圓C的極坐標方程為:
在以O為極點,以x 軸的正半軸為極軸的極坐標系中,圓C的極坐標方程為:
(Ⅰ)將直線l的參數方程化為普通方程,圓C的極坐標方程化為直角坐標方程;
(Ⅱ)判斷直線 與圓C的位置關系.
與圓C的位置關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com