
【題目】如圖,四邊形ABCD內(nèi)接于⊙O,過點A作⊙O的切線EP交CB的延長線于P,∠PAB=35°. 
(1)若BC是⊙O的直徑,求∠D的大小;
(2)若∠PAB=35°,求證: ![]() .
.
【答案】
(1)解:∵EP與⊙O相切于點A,∴∠ACB=∠PAB=35°,
又BC是⊙O的直徑,∴∠ABC=55°.
∵四邊形ABCD內(nèi)接于⊙O,∴∠ABC+∠D=180°,
∴∠D=112°
(2)證明:∵∠DAE=35°,
∴∠ACD=∠PAB,∠D=∠PBA,
∴△ADC∽△ABP,
∴ ![]() =
= ![]() ,∠DBA=∠BDA,
,∠DBA=∠BDA,
∴DA=BA,∴DA2=DCBP,AP2=PCBP,
∴ ![]()
【解析】(1)由弦切角定理得∠ACB=∠PAB=25°,從而∠ABC=65°,由此利用四邊形ABCD內(nèi)接于⊙O,能求出∠D.(2)由∠DAE=25°,∠ACD=∠PAB,∠D=∠PBA,從而△ADC∽△PBA,由此能證明DA2=DCBP,AP2=PCBP,即可證明結(jié)論.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() :若
:若![]() ,則
,則![]() ,下列說法正確的是( )
,下列說法正確的是( )
A. 命題![]() 的否命題是“若
的否命題是“若![]() ,則
,則![]() ”
”
B. 命題![]() 的逆否命題是“若
的逆否命題是“若![]() ,則
,則![]() ”
”
C. 命題![]() 是真命題
是真命題
D. 命題![]() 的逆命題是真命題
的逆命題是真命題
【答案】D
【解析】A. 命題![]() 的否命題是若
的否命題是若![]()
B. 命題![]() 的逆否命題是“若
的逆否命題是“若![]() ,則
,則![]()
![]()
C. 命題![]() 是假命題,比如當(dāng)x=-3,就不滿足條件,故選項不正確.
是假命題,比如當(dāng)x=-3,就不滿足條件,故選項不正確.
D. 命題![]() 的逆命題是若
的逆命題是若![]() 是真命題.
是真命題.
故答案為:D.
【題型】單選題
【結(jié)束】
9
【題目】“雙曲線的方程為![]() ”是“雙曲線的漸近線方程為
”是“雙曲線的漸近線方程為![]() ”的( )
”的( )
A. 充分不必要條件 B. 必要不充分條件
C. 充分必要條件 D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 的內(nèi)角
的內(nèi)角![]() ,
, ![]() ,
, ![]() 所對的邊分別為
所對的邊分別為![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的值;
的值;
(2)當(dāng)![]() 的面積為
的面積為![]() 時,求
時,求![]() 的周長.
的周長.
【答案】(1) ![]() (2)8
(2)8
【解析】試題分析:(1)由![]() ,
, ![]() ,由正弦定理得到
,由正弦定理得到![]() ;(2)根據(jù)面積公式得到
;(2)根據(jù)面積公式得到![]() ,再由余弦定理得到
,再由余弦定理得到![]() ,進(jìn)而得到
,進(jìn)而得到![]() .
.
解析:
(1)因為![]() ,所以
,所以![]()
由正弦定理![]() ,可得
,可得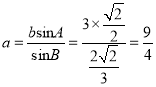
(2)因為![]() 的面積
的面積![]()
所以![]()
由余弦定理![]()
得![]() ,即
,即![]()
所以![]() ,
,
所以![]()
所以, ![]() 的周長為
的周長為![]()
【題型】解答題
【結(jié)束】
18
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() .
.
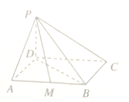
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,求直線
的中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,并且滿足
,并且滿足![]() ,
, ![]() .
.
(1)求數(shù)列![]() 通項公式;
通項公式;
(2)設(shè)![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項和,求證:
項和,求證: ![]() .
.
【答案】(1) ![]() (2)見解析
(2)見解析
【解析】試題分析:(1)根據(jù)題意得到![]() ,
, ![]() ,兩式做差得到
,兩式做差得到![]() ;(2)根據(jù)第一問得到
;(2)根據(jù)第一問得到![]() ,由錯位相減法得到前n項和,進(jìn)而可證和小于1.
,由錯位相減法得到前n項和,進(jìn)而可證和小于1.
解析:
(1)∵![]()
當(dāng)![]() 時,
時, ![]()
當(dāng)![]() 時,
時, ![]() ,即
,即![]()
∴數(shù)列![]() 時以
時以![]() 為首項,
為首項, ![]() 為公差的等差數(shù)列.
為公差的等差數(shù)列.
∴![]() .
.
(2)∵![]()
∴![]() ①
①
![]() ②
②
由①![]() ②得
②得
![]()
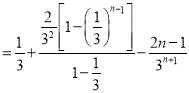
![]()
∴![]()
點睛:這個題目考查的是數(shù)列通項公式的求法及數(shù)列求和的常用方法;數(shù)列通項的求法中有常見的已知![]() 和
和![]() 的關(guān)系,求
的關(guān)系,求![]() 表達(dá)式,一般是寫出
表達(dá)式,一般是寫出![]() 做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數(shù)列求和常用法有:錯位相減,裂項求和,分組求和等.
做差得通項,但是這種方法需要檢驗n=1時通項公式是否適用;數(shù)列求和常用法有:錯位相減,裂項求和,分組求和等.
【題型】解答題
【結(jié)束】
22
【題目】已知![]() ,
, ![]() 分別是橢圓
分別是橢圓![]() :
: ![]() (
(![]() )的左、右焦點,
)的左、右焦點, ![]() 是橢圓
是橢圓![]() 上的一點,且
上的一點,且![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若直線![]() :
: ![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
, ![]() ,橢圓
,橢圓![]() 上存在點
上存在點![]() ,使得以
,使得以![]() ,
, ![]() 為鄰邊的四邊形
為鄰邊的四邊形![]() 為平行四邊形(
為平行四邊形(![]() 為坐標(biāo)原點).
為坐標(biāo)原點).
(ⅰ)求實數(shù)![]() 與
與![]() 的關(guān)系;
的關(guān)系;
(ⅱ)證明:四邊形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知實數(shù)a、m滿足a= ![]() cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 則m=( )
cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 則m=( )
A.﹣1或3
B.1或﹣3
C.1
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,頂點A(a,0),B(0,b),中心O到直線AB的距離為
,頂點A(a,0),B(0,b),中心O到直線AB的距離為 ![]() .
.
(1)求橢圓C的方程;
(2)設(shè)橢圓C上一動點P滿足: ![]() ,其中M,N是橢圓C上的點,直線OM與ON的斜率之積為﹣
,其中M,N是橢圓C上的點,直線OM與ON的斜率之積為﹣ ![]() ,若Q(λ,μ)為一動點,E1(﹣
,若Q(λ,μ)為一動點,E1(﹣ ![]() ,0),E2(
,0),E2( ![]() ,0)為兩定點,求|QE1|+|QE2|的值.
,0)為兩定點,求|QE1|+|QE2|的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com