
已知 為坐標(biāo)原點,且
為坐標(biāo)原點,且 ,則
,則 點的坐標(biāo)為 .
點的坐標(biāo)為 .
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分12分)已知![]() 為坐標(biāo)原點,向量
為坐標(biāo)原點,向量![]() ,點是直線
,點是直線![]() 上的一點,且點分有向線段
上的一點,且點分有向線段![]() 的比為.(1)記函數(shù)
的比為.(1)記函數(shù)![]() ,
,![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)性,并求其值域;(2)若
的單調(diào)性,并求其值域;(2)若![]() 三點共線,求
三點共線,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本題滿分18分,其中第1小題5分,第2小題5分,第3小題8分)
在平面直角坐標(biāo)系中,已知![]() 為坐標(biāo)原點,點
為坐標(biāo)原點,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點
,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,其中
,其中![]() 且
且![]() .設(shè)
.設(shè)![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的解集;
內(nèi)的解集;
(2)若點![]() 是過點
是過點![]() 且法向量為
且法向量為![]() 的直線
的直線![]() 上的動點.當(dāng)
上的動點.當(dāng)![]() 時,設(shè)函數(shù)
時,設(shè)函數(shù)![]() 的值域為集合
的值域為集合![]() ,不等式
,不等式![]() 的解集為集合
的解集為集合![]() . 若
. 若![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大值;
的最大值;
(3)根據(jù)本題條件我們可以知道,函數(shù)![]() 的性質(zhì)取決于變量
的性質(zhì)取決于變量![]() 、
、![]() 和
和![]() 的值. 當(dāng)
的值. 當(dāng)![]() 時,試寫出一個條件,使得函數(shù)
時,試寫出一個條件,使得函數(shù)![]() 滿足“圖像關(guān)于點
滿足“圖像關(guān)于點![]() 對稱,且在
對稱,且在![]() 處
處![]() 取得最小值”.(說明:請寫出你的分析過程.本小題將根據(jù)你對問題探究的完整性和在研究過程中所體現(xiàn)的思維層次,給予不同的評分.)
取得最小值”.(說明:請寫出你的分析過程.本小題將根據(jù)你對問題探究的完整性和在研究過程中所體現(xiàn)的思維層次,給予不同的評分.)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分12分)已知![]() 為坐標(biāo)原點,
為坐標(biāo)原點,![]() 其中
其中![]() 為常數(shù),設(shè)函數(shù)
為常數(shù),設(shè)函數(shù)![]() .
.
(1)求函數(shù)![]() 的表達(dá)式和最小正周期;
的表達(dá)式和最小正周期;
(2)若角![]() 為
為![]() 的三個內(nèi)角中的最大角且
的三個內(nèi)角中的最大角且![]() 的最小值為
的最小值為![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,試畫出![]() 的簡圖.
的簡圖.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:廣州省2009-2010學(xué)年高二學(xué)科競賽(數(shù)學(xué)理) 題型:解答題
(本小題滿分14分)已知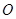 為坐標(biāo)原點,點F、T、M、P分別滿足
為坐標(biāo)原點,點F、T、M、P分別滿足 .
.
(1) 當(dāng)t 變化時,求點P的軌跡方程;
(2) 若 的頂點在點P的軌跡上,且點A的縱坐標(biāo)
的頂點在點P的軌跡上,且點A的縱坐標(biāo)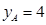 ,
, 的重心恰好為點F,
的重心恰好為點F,
求直線BC的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com