
 ʼ�Kƽ�ֈA
ʼ�Kƽ�ֈA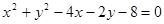 �����L���t
�����L���t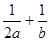 ����Сֵ��
����Сֵ��A��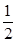 | B�� | C�� | D�� |
 �����Ļ��옷�����h������ϵ�д�
�����Ļ��옷�����h������ϵ�д� ��(y��u)�����옷����ÿһ��ȫ�º������I(y��)��ϵ�д�
��(y��u)�����옷����ÿһ��ȫ�º������I(y��)��ϵ�д� ��ٽ���ِ�½������������ϵ�д�
��ٽ���ِ�½������������ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
 �^���c(di��n)
�^���c(di��n)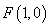 ,���c��ֱ��
,���c��ֱ��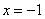 ����.
����. ��܉�E
��܉�E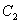 �ķ��̣�
�ķ��̣�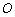 �ęE�A
�ęE�A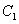 ��һ�����c(di��n)��
��һ�����c(di��n)��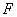 ,ֱ���^�c(di��n)
,ֱ���^�c(di��n)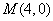 .������(bi��o)ԭ�c(di��n)
.������(bi��o)ԭ�c(di��n)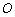 �P(gu��n)��ֱ���Č��Q�c(di��n)
�P(gu��n)��ֱ���Č��Q�c(di��n)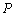 ������
������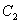 �ϣ���ֱ���c�E�A
�ϣ���ֱ���c�E�A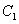 �й����c(di��n),��E�A
�й����c(di��n),��E�A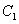 ���L�S�Lȡ����Сֵ�r�ęE�A����.
���L�S�Lȡ����Сֵ�r�ęE�A����. �鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
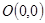 �ĈAC�cֱ��
�ĈAC�cֱ��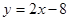 �������c(di��n)
�������c(di��n)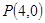 .
.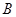 ������(bi��o)��
������(bi��o)��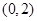 ���O(sh��)
���O(sh��)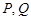 �քe��ֱ��
�քe��ֱ��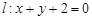 �͈A
�͈A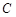 �ϵĄ��c(di��n)����
�ϵĄ��c(di��n)����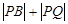 ����Сֵ��
����Сֵ��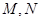 �P(gu��n)��ֱ��
�P(gu��n)��ֱ��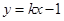 ���Q������
���Q������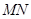 ��ֱ���ĈA��(j��ng)�^ԭ�c(di��n)�������ڣ�����ֱ��
��ֱ���ĈA��(j��ng)�^ԭ�c(di��n)�������ڣ�����ֱ��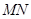 �ķ��̣��������ڣ��f������.
�ķ��̣��������ڣ��f������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
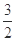 ,3)��ֱ�������A
,3)��ֱ�������A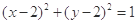 ��A��B���c(di��n)��Q��A������һ�c(di��n)����Q��AB�������x��
��A��B���c(di��n)��Q��A������һ�c(di��n)����Q��AB�������x��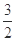 ���tֱ��l�ķ��̞� ��
���tֱ��l�ķ��̞� ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
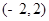 ���돽��5�ĈA�Ę�(bi��o)��(zh��n)���̞飨 ��
���돽��5�ĈA�Ę�(bi��o)��(zh��n)���̞飨 ��A�� | B�� |
C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
A��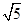 | B��10 | C��9 | D��5+2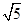 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
| A��4 | B��4 | C��8 | D��8 |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com