【答案】
分析:(1)依題意,利用等比數列前n項和公式可以出一個方程組,解這個方程組,得到數列{a
n}的首項a
1和公比q.
(2)由
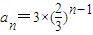
,知數列T
(2)的首項為t
1=a
2=2,公差d=2a
2-1=3,由此能求出T
(2)的前2007項之和.
(3)(理)b
i=a
i+(i-1)(2a
i-1)=(2i-1)a
i-(i-1)=
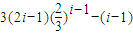
;①
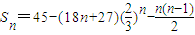
;由此計算得
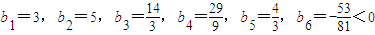
,所以S
n當n=5時取最大值.②
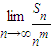
=
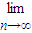
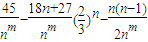
,由此分類討論進行求解.
(文)b
i=a
i+(i-1)(2a
i-1)=(2i-1)a
i-(i-1)=

;
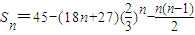
;
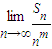
=
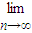
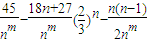
,由此分類討論進行求解.
解答:解:(1)依題意可知,
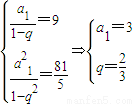
.
(2)由(1)知,
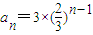
,所以數列T
(2)的首項為t
1=a
2=2,公差d=2a
2-1=3,
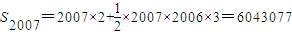
,即數列的前2007項之和為6043077.
(3)(理)b
i=a
i+(i-1)(2a
i-1)=(2i-1)a
i-(i-1)=
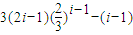
;
①
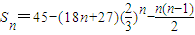
;
由
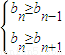
,解得n=2,
計算可得
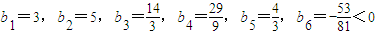
,
因為當n≥2時,b
n>b
n+1,所以S
n當n=5時取最大值.
②
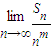
=
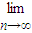
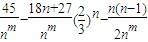
,
當m=2時,
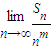
=-

,當m>2時,

=0,所以m=2.
(文)b
i=a
i+(i-1)(2a
i-1)=(2i-1)a
i-(i-1)=
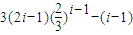
;
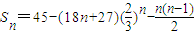
;
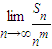
=
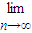
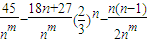
,
當m=2時,
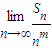
=-

,當m>2時,
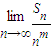
=0,所以m=2.
點評:本題考查數列的極限和運算,解題時要認真審題,仔細解答,注意公式的合理運用.

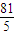 .
.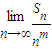 存在且不等于零.
存在且不等于零.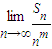 存在且不等于零.
存在且不等于零.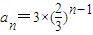 ,知數列T(2)的首項為t1=a2=2,公差d=2a2-1=3,由此能求出T(2)的前2007項之和.
,知數列T(2)的首項為t1=a2=2,公差d=2a2-1=3,由此能求出T(2)的前2007項之和.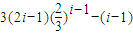 ;①
;①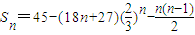 ;由此計算得
;由此計算得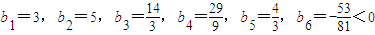 ,所以Sn當n=5時取最大值.②
,所以Sn當n=5時取最大值.②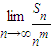 =
=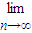
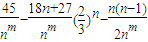 ,由此分類討論進行求解.
,由此分類討論進行求解. ;
;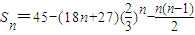 ;
;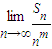 =
=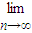
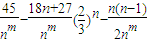 ,由此分類討論進行求解.
,由此分類討論進行求解.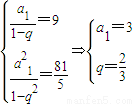 .
.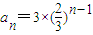 ,所以數列T(2)的首項為t1=a2=2,公差d=2a2-1=3,
,所以數列T(2)的首項為t1=a2=2,公差d=2a2-1=3,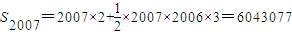 ,即數列的前2007項之和為6043077.
,即數列的前2007項之和為6043077.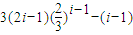 ;
;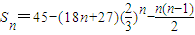 ;
;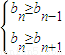 ,解得n=2,
,解得n=2,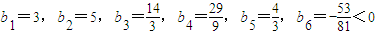 ,
,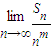 =
=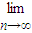
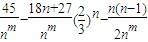 ,
,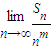 =-
=- ,當m>2時,
,當m>2時, =0,所以m=2.
=0,所以m=2.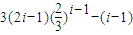 ;
;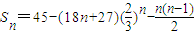 ;
;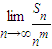 =
=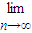
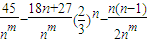 ,
,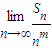 =-
=- ,當m>2時,
,當m>2時,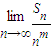 =0,所以m=2.
=0,所以m=2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案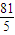 .
.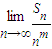 存在且不等于零.
存在且不等于零.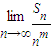 存在且不等于零.
存在且不等于零.