
【題目】為篩查在人群中傳染的某種病毒,現(xiàn)有兩種檢測(cè)方法:
(1)抗體檢測(cè)法:每個(gè)個(gè)體獨(dú)立檢測(cè),每一次檢測(cè)成本為80元,每個(gè)個(gè)體收取檢測(cè)費(fèi)為100元.
(2)核酸檢測(cè)法:先合并個(gè)體,其操作方法是:當(dāng)個(gè)體不超過(guò)10個(gè)時(shí),把所有個(gè)體合并在一起進(jìn)行檢測(cè).
當(dāng)個(gè)體超過(guò)10個(gè)時(shí),每10個(gè)個(gè)體為一組進(jìn)行檢測(cè).若該組檢測(cè)結(jié)果為陰性(正常),則只需檢測(cè)一次;若該組檢測(cè)結(jié)果為陽(yáng)性(不正常),則需再對(duì)每個(gè)個(gè)體按核酸檢測(cè)法重新獨(dú)立檢測(cè),共需檢測(cè)k+1次(k為該組個(gè)體數(shù),1≤k≤10,k∈N*).每一次檢測(cè)成本為160元.假設(shè)在接受檢測(cè)的個(gè)體中,每個(gè)個(gè)體的檢測(cè)結(jié)果是陽(yáng)性還是陰性相互獨(dú)立,且每個(gè)個(gè)體是陽(yáng)性結(jié)果的概率均為p(0<p<1).
(Ⅰ)現(xiàn)有100個(gè)個(gè)體采取抗體檢測(cè)法,求其中恰有一個(gè)檢測(cè)出為陽(yáng)性的概率;
(Ⅱ)因大多數(shù)人群篩查出現(xiàn)陽(yáng)性的概率很低,且政府就核酸檢測(cè)法給子檢測(cè)機(jī)構(gòu)一定的補(bǔ)貼,故檢測(cè)機(jī)構(gòu)推出組團(tuán)選擇核酸檢測(cè)優(yōu)惠政策如下:無(wú)論是檢測(cè)一次還是k+1次,每組所有個(gè)體共收費(fèi)700元(少于10個(gè)個(gè)體的組收費(fèi)金額不變).已知某企業(yè)現(xiàn)有員工107人,準(zhǔn)備進(jìn)行全員檢測(cè),擬準(zhǔn)備9000元檢測(cè)費(fèi),由于時(shí)間和設(shè)備條件的限制,采用核酸檢測(cè)法合并個(gè)體的組數(shù)不得高于參加采用抗體檢測(cè)法人數(shù),請(qǐng)?jiān)O(shè)計(jì)一個(gè)合理的的檢測(cè)安排方案;
(Ⅲ)設(shè)![]() ,現(xiàn)有n(n∈N*且2≤n≤10)個(gè)個(gè)體,若出于成本考慮,僅采用一種檢測(cè)方法,試問(wèn)檢測(cè)機(jī)構(gòu)應(yīng)采用哪種檢測(cè)方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
,現(xiàn)有n(n∈N*且2≤n≤10)個(gè)個(gè)體,若出于成本考慮,僅采用一種檢測(cè)方法,試問(wèn)檢測(cè)機(jī)構(gòu)應(yīng)采用哪種檢測(cè)方法?(ln3≈1.099,ln4≈1.386,ln5≈1.609,ln6≈1.792)
【答案】(Ⅰ)![]() .(Ⅱ)見(jiàn)解析(Ⅲ)當(dāng)n=2時(shí),采用抗體檢測(cè)法,當(dāng)3≤n≤10,n∈N*時(shí),采用核酸檢測(cè)法.
.(Ⅱ)見(jiàn)解析(Ⅲ)當(dāng)n=2時(shí),采用抗體檢測(cè)法,當(dāng)3≤n≤10,n∈N*時(shí),采用核酸檢測(cè)法.
【解析】
(Ⅰ)利用n次獨(dú)立重復(fù)試驗(yàn)中事件A恰好發(fā)生k次概率計(jì)算公式能求出其中恰有一個(gè)檢測(cè)出為陽(yáng)性的概率;(Ⅱ)設(shè)安排x個(gè)個(gè)體采用抗體檢測(cè)法,y組個(gè)體采用核酸檢測(cè)法,根據(jù)已知條件列出不等式組,總檢測(cè)費(fèi)用為z=100x+700y,利用線性規(guī)劃設(shè)計(jì)合理的安排方案;(Ⅲ)分別求出兩種檢測(cè)法的成本期望,由EX>EY推導(dǎo)出ln(![]() )
)![]() ,利用導(dǎo)數(shù)研究函數(shù)
,利用導(dǎo)數(shù)研究函數(shù)![]() 的單調(diào)性從而求出n的取值范圍,即可確定檢測(cè)方法.
的單調(diào)性從而求出n的取值范圍,即可確定檢測(cè)方法.
(Ⅰ)現(xiàn)有100個(gè)個(gè)體采取抗體檢測(cè)法,其中恰有一個(gè)檢測(cè)出為陽(yáng)性的概率為:
P![]() .
.
(Ⅱ)設(shè)安排x個(gè)個(gè)體采用抗體檢測(cè)法,y組個(gè)體采用核酸檢測(cè)法,
則由條件知: ,x,y∈N,
,x,y∈N,
總檢測(cè)費(fèi)用為![]() .
.
畫(huà)出可行域如圖,
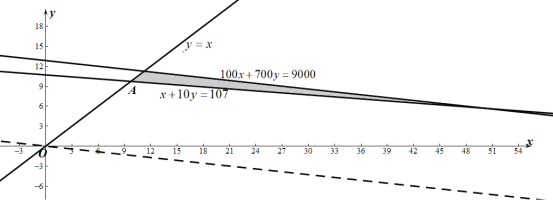
由![]() ,解得A(
,解得A(![]() ,
,![]() ),
),
則在可行域內(nèi)臨近A點(diǎn)的整點(diǎn)有(10,10),(17,9),此時(shí),Zmin=8000,
即安排17人采取抗體檢測(cè)法,90人采用核酸檢測(cè)法,或者安排10人采取抗體檢測(cè)法,97人采用核酸檢測(cè)法,可使所有員工參加檢測(cè),且費(fèi)用偏低.
(Ⅲ)設(shè)采用抗體檢測(cè)法,檢測(cè)機(jī)構(gòu)成本期望為EX,則![]() ,
,
采用核酸檢測(cè),檢測(cè)機(jī)構(gòu)成本期望為EY,
設(shè)采用核酸檢測(cè)法檢測(cè)次數(shù)為η,則η的取值只有1和n+1,
且![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
設(shè)EX>EY,則![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]()
![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
由![]() ,得
,得![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又![]()
![]() ,
,
![]() ,
,
∴當(dāng)n≥3,![]() 時(shí),EX>EY,
時(shí),EX>EY,
∴當(dāng)n=2時(shí),采用抗體檢測(cè)法,當(dāng)3≤n≤10,![]() 時(shí),采用核酸檢測(cè)法.
時(shí),采用核酸檢測(cè)法.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形ABCD是矩形,平面
中,四邊形ABCD是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,E是SB的中點(diǎn),M是CD上任意一點(diǎn).
,E是SB的中點(diǎn),M是CD上任意一點(diǎn).
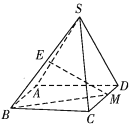
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 平面SAD,求直線BM與平面SAB所成角的正弦值.
平面SAD,求直線BM與平面SAB所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)有甲,乙兩種不透明充氣包裝的袋裝零食,每袋零食甲隨機(jī)附贈(zèng)玩具![]() ,
,![]() ,
,![]() 中的一個(gè),每袋零食乙從玩具
中的一個(gè),每袋零食乙從玩具![]() ,
,![]() 中隨機(jī)附贈(zèng)一個(gè).記事件
中隨機(jī)附贈(zèng)一個(gè).記事件![]() :一次性購(gòu)買(mǎi)
:一次性購(gòu)買(mǎi)![]() 袋零食甲后集齊玩具
袋零食甲后集齊玩具![]() ,
,![]() ,
,![]() ;事件
;事件![]() :一次性購(gòu)買(mǎi)
:一次性購(gòu)買(mǎi)![]() 袋零食乙后集齊玩具
袋零食乙后集齊玩具![]() ,
,![]() .
.
(1)求概率![]() ,
,![]() 及
及![]() ;
;
(2)已知![]() ,其中
,其中![]() ,
,![]() 為常數(shù),求
為常數(shù),求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,AB⊥側(cè)面BCC1B1,AC=AB1.
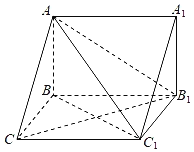
(1)求證:平面ABC1⊥平面AB1C;
(2)若AB=BC=2,∠BCC1=60°,求二面角B﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
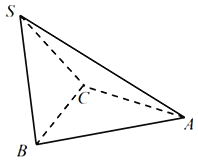
【題目】如圖所示,三棱錐S一ABC中,△ABC與△SBC都是邊長(zhǎng)為1的正三角形,二面角A﹣BC﹣S的大小為![]() ,若S,A,B,C四點(diǎn)都在球O的表面上,則球O的表面積為( )
,若S,A,B,C四點(diǎn)都在球O的表面上,則球O的表面積為( )
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 只有
只有![]() 個(gè)正整數(shù)解,求
個(gè)正整數(shù)解,求![]() 的取值范圍;
的取值范圍;
(2)①求證:方程![]() 有唯一實(shí)根
有唯一實(shí)根![]() ,且
,且![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() 為正項(xiàng)數(shù)列
為正項(xiàng)數(shù)列![]() 的前
的前![]() 項(xiàng)和,滿足
項(xiàng)和,滿足![]() .
.
(1)求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若不等式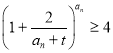 對(duì)任意正整數(shù)
對(duì)任意正整數(shù)![]() 都成立,求實(shí)數(shù)
都成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() (其中
(其中![]() 是自然對(duì)數(shù)的底數(shù)),求證:
是自然對(duì)數(shù)的底數(shù)),求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知不等式組 表示的平面區(qū)域?yàn)?/span>
表示的平面區(qū)域?yàn)?/span>![]() ,若函數(shù)
,若函數(shù)![]() 的圖象上存在區(qū)域
的圖象上存在區(qū)域![]() 內(nèi)的點(diǎn),則實(shí)數(shù)
內(nèi)的點(diǎn),則實(shí)數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,G為
,G為![]() 的中點(diǎn),正方形
的中點(diǎn),正方形![]() 與平行四邊形
與平行四邊形![]() 所在的平面互相垂直.
所在的平面互相垂直.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com