
【題目】根據某電子商務平臺的調查統計顯示,參與調查的1000位上網購物者的年齡情況如圖顯示. 
(1)已知[30,40)、[40,50)、[50,60)三個年齡段的上網購物者人數成等差數列,求a,b的值.
(2)該電子商務平臺將年齡在[30,50)之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發放代金券,高消費人群每人發放50元的代金券,潛在消費人群每人發放100元的代金券,現采用分層抽樣的方式從參與調查的1000位上網購者中抽取10人,并在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和X的分布列與數學期望.
【答案】
(1)解:∵[30,40)、[40,50)、[50,60)三個年齡段的上網購物者人數成等差數列,
∴由頻率分布直方圖得 ![]() ,
,
解得a=0.035,b=0.025
(2)解:利用分層抽樣從樣本中抽取10人,
其中屬于高消費人群的為6人,屬于潛在消費人群的為4人.
從中取出三人,并計算三人所獲得代金券的總和X,
則X的所有可能取值為:150,200,250,300.
P(X=150)= 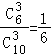 ,
,
P(X=200)= 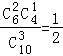 ,
,
P(X=250)= 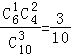 ,
,
P(X=300)= 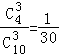 ,
,
∴X的分布列為:
X | 150 | 200 | 250 | 300 |
P |
|
|
|
|
EX=150× ![]() +200×
+200× ![]() +250×
+250× ![]() +300×
+300× ![]() =210.
=210.
【解析】(1)由等差數列性質和頻率分布直方圖得 ![]() ,由此能求出a,b.(2)利用分層抽樣從樣本中抽取10人,其中屬于高消費人群的為6人,屬于潛在消費人群的為4人.從中取出三人,并計算三人所獲得代金券的總和X,則X的所有可能取值為:150,200,250,300.分別求出相應的概率,由此能求出此三人獲得代金券總和X的分布列與數學期望
,由此能求出a,b.(2)利用分層抽樣從樣本中抽取10人,其中屬于高消費人群的為6人,屬于潛在消費人群的為4人.從中取出三人,并計算三人所獲得代金券的總和X,則X的所有可能取值為:150,200,250,300.分別求出相應的概率,由此能求出此三人獲得代金券總和X的分布列與數學期望
【考點精析】關于本題考查的頻率分布直方圖和離散型隨機變量及其分布列,需要了解頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息;在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列才能得出正確答案.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:
【題目】《張丘建算經》是我國南北朝時期的一部重要數學著作,書中系統的介紹了等差數列,同類結果在三百多年后的印度才首次出現.書中有這樣一個問題,大意為:某女子善于織布,后一天比前一天織的快,而且每天增加的數量相同,已知第一天織布5尺,一個月(按30天計算)總共織布390尺,問每天增加的數量為多少尺?該問題的答案為( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() 過點
過點![]() 且與圓
且與圓![]() 相切 .
相切 .
(I)求直線![]() 的方程;
的方程;
(II)如圖,圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,點
兩點,點![]() 是圓
是圓![]() 上異于
上異于![]() 的任意一點,過點
的任意一點,過點![]() 且與
且與![]() 軸垂直的直線為
軸垂直的直線為![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,求證:以
,求證:以![]() 為直徑的圓
為直徑的圓![]() 與
與![]() 軸交于定點
軸交于定點![]() ,并求出點
,并求出點![]() 的坐標 .
的坐標 .

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前北方空氣污染越來越嚴重,某大學組織學生參加環保知識競賽,從參加學生中抽取40名,將其成績(均為整數)整理后畫出的頻率分布直方圖如圖,若從成績是80分以上(包括80分)的學生中選兩人,則他們在同一分數段的概率為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,直線
的焦點為F,直線![]() 與x軸的交點為P,與拋物線的交點為Q,且
與x軸的交點為P,與拋物線的交點為Q,且![]() .
.

![]() 求拋物線的方程;
求拋物線的方程;
![]() 如圖所示,過F的直線l與拋物線相交于
如圖所示,過F的直線l與拋物線相交于![]() 兩點,與圓
兩點,與圓![]() 相交于
相交于![]() 兩點
兩點![]() 兩點相鄰
兩點相鄰![]() ,過
,過![]() 兩點分別作拋物線的切線,兩條切線相交于點M,求
兩點分別作拋物線的切線,兩條切線相交于點M,求![]() 與
與![]() 的面積之積的最小值.
的面積之積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩支排球隊進行比賽,先勝3局者獲得比賽的勝利,比賽隨即結束.除第五局甲隊獲勝的概率是 ![]() ,其余每局比賽甲隊獲勝的概率都是
,其余每局比賽甲隊獲勝的概率都是 ![]() .設各局比賽結果相互獨立.
.設各局比賽結果相互獨立.
(1)分別求甲隊3:0,3:1,3:2勝利的概率;
(2)若比賽結果3:0或3:1,則勝利方得3分,對方得0分;若比賽結果為3:2,則勝利方得2分,對方得1分,求乙隊得分X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,F1 , F2分別為橢圓 ![]() +
+ ![]() =1(a>b>0)的左、右焦點,頂點B的坐標為(0,b),連接BF2并延長交橢圓于點A,過點A作x軸的垂線交橢圓于另一點C,連接F1C.
=1(a>b>0)的左、右焦點,頂點B的坐標為(0,b),連接BF2并延長交橢圓于點A,過點A作x軸的垂線交橢圓于另一點C,連接F1C. 
(1)若點C的坐標為( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求橢圓的方程;
,求橢圓的方程;
(2)若F1C⊥AB,求橢圓離心率e的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com