【題目】關于實數x的不等式﹣x2+bx+c＜0的解集是{x|x＜﹣3或x＞2}，則關于x的不等式cx2﹣bx﹣1＞0的解集是（ ）
A.（﹣ 
， 
）
B.（﹣2，3）
C.（﹣∞，﹣ ）∪（ ，+∞）
D.（﹣∞，﹣2）∪（3，+∞）
【答案】C
【解析】解：關于x的不等式﹣x2+bx+c＜0的解集是{x|x＜﹣3或x＞2}， ∴對應方程﹣x2+bx+c=0的兩個實數根為﹣3和2，
由根與系數的關系，得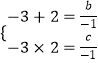
，
解得b=﹣1，c=6；
∴關于x的不等式cx2﹣bx﹣1＞0可化為
6x2+x﹣1＞0，
解得x＜﹣ 
或x＞ 
；
∴該不等式的解集是（﹣∞，﹣ ）∪（ ，+∞）．
故選：C．
【考點精析】利用解一元二次不等式對題目進行判斷即可得到答案，需要熟知求一元二次不等式
解集的步驟：一化：化二次項前的系數為正數;二判：判斷對應方程的根;三求：求對應方程的根;四畫：畫出對應函數的圖象;五解集：根據圖象寫出不等式的解集;規律：當二次項系數為正時，小于取中間，大于取兩邊．
科目：高中數學 來源： 題型：
【題目】動點P，Q從點A（1，0）出發沿單位圓運動，點P按逆時針方向每秒鐘轉 
弧度，點Q按順時針方向每秒鐘轉 
弧度，設P，Q第一次相遇時在點B，則B點的坐標為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是正方體的平面展開圖，在這個正方體中， ①BM與ED平行；
②CN與BE是異面直線；
③CN與BM成60°角；
④DM與BN垂直．
以上四個命題中，正確命題的序號是（ ）
A.③
B.③④
C.①③
D.①③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓C： 
+ 
=1（a＞b＞0）的離心率為 
，其左焦點到點P（2，1）的距離為 
． （Ⅰ）求橢圓C的標準方程；
（Ⅱ）若直線l：y=kx+m與橢圓C相交于A，B兩點（A，B不是左右頂點），且以AB為直徑的圓過橢圓C的右頂點．求證：直線l過定點，并求出該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線E的中心為原點，P（3，0）是E的焦點，過P的直線l與E相交于A，B兩點，且AB的中點為N（﹣12，﹣15），則E的方程式為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，AB=1，AC=2，BC= 
，D，E分別是AC1和BB1的中點，則直線DE與平面BB1C1C所成的角為（ ） 
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了促進學生的全面發展，鄭州市某中學重視學生社團文化建設，現用分層抽樣的方法從“話劇社”，“創客社”，“演講社”三個金牌社團中抽取6人組成社團管理小組，有關數據見表（單位：人）：
社團名稱 | 成員人數 | 抽取人數 |
話劇社 | 50 | a |
創客社 | 150 | b |
演講社 | 100 | c |
（1）求a，b，c的值；
（2）若從“話劇社”，“創客社”，“演講社”已抽取的6人中任意抽取2人擔任管理小組組長，求這2人來自不同社團的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】三棱錐ABCD中，BC=DC=AB=AD= 
，BD=2，平面ABD⊥平面BCD，O為BD的中點，P、Q分別為線段AO，BC上的動點，且AP=CQ，求三棱錐PQCO體積的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
