

去截圓錐,證明這個平面與圓錐的交線是一個橢圓.
思路點撥:
運用Dandelin雙球討論證明.
證明:如圖,在圓錐內部嵌入Dandelin雙球,一個位于平面π的上方,一個位于平面π的下方,并且與平面π均相切.
當平面π與底面的夾角β大于圓錐母線與底面的夾角時,平面π與圓錐的交線是一條封閉曲線.
設兩個球與平面π的切點分別為F1、F2,與圓錐相切于圓S1、S2,在截口的曲線上任取一點P,連結PF1、PF2,過P作母線交S1于Q1,S2于Q2.
于是PF1和PQ1是從P到上方球的兩條切線,因此,PF1=PQ1,同理,PF2=PQ2.
∴PF1+PF2=PQ1+PQ2=Q1Q2.
由正圓錐的對稱性,Q1Q2的長度等于兩圓S1、S2所在平行平面間的母線段的長度,與P的位置無關.
由此我們可以斷定截口的曲線是以F1、F2為焦點的橢圓.


科目:高中數學 來源:2012-2013學年福建省畢業班質量檢查文科數學試卷(解析版) 題型:解答題
某同學用《幾何畫板》研究拋物線的性質:打開《幾何畫板》軟件,繪制某拋物線 ,在拋物線上任意畫一個點
,在拋物線上任意畫一個點 ,度量點
,度量點 的坐標
的坐標 ,如圖.
,如圖.

(Ⅰ)拖動點 ,發現當
,發現當 時,
時, ,試求拋物線
,試求拋物線 的方程;
的方程;
(Ⅱ)設拋物線 的頂點為
的頂點為 ,焦點為
,焦點為 ,構造直線
,構造直線 交拋物線
交拋物線 于不同兩點
于不同兩點 、
、 ,構造直線
,構造直線 、
、 分別交準線于
分別交準線于 、
、 兩點,構造直線
兩點,構造直線 、
、 .經觀察得:沿著拋物線
.經觀察得:沿著拋物線 ,無論怎樣拖動點
,無論怎樣拖動點 ,恒有
,恒有
 .請你證明這一結論.
.請你證明這一結論.
(Ⅲ)為進一步研究該拋物線 的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點
的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點 ”改變為其它“定點
”改變為其它“定點
 ”,其余條件不變,發現“
”,其余條件不變,發現“ 與
與 不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
 ”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市松江區高三5月模擬考試文科數學 題型:填空題
用一個不平行于底面的平面截一個底面直徑為40 的圓柱,截得如圖幾何體,若截面橢圓的長軸為50
的圓柱,截得如圖幾何體,若截面橢圓的長軸為50 ,幾何體最短的母線長為70
,幾何體最短的母線長為70 ,則此幾何體的體積為
▲
,則此幾何體的體積為
▲ 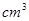 .
.

查看答案和解析>>
科目:高中數學 來源:2011屆上海市松江區高三5月模擬考試文科數學 題型:填空題
用一個不平行于底面的平面截一個底面直徑為40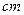 的圓柱,截得如圖幾何體,若截面橢圓的長軸為50
的圓柱,截得如圖幾何體,若截面橢圓的長軸為50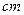 ,幾何體最短的母線長為70
,幾何體最短的母線長為70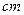 ,則此幾何體的體積為 ▲
,則此幾何體的體積為 ▲  .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com