
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 銷售量x(萬件) | 10 | 11 | 13 | 12 | 8 | 6 |
| 利潤y(萬元) | 22 | 25 | 29 | 26 | 16 | 12 |
分析 (1)求出$\overline{x}$,$\overline{y}$,由公式,得$\widehat{b}$的值,從而求出$\widehat{a}$的值,從而得到y關于x的線性回歸方程,
(2)由(1)能求出該小組所得線性回歸方程是理想的.
解答 解:(1)∵$\overline{x}$=11,$\overline{y}$=24,
∴$\widehat{b}$=$\frac{18}{7}$,
故$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=-$\frac{30}{7}$,
故y關于x的方程是:$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$;
(2)∵x=10時,$\widehat{y}$=$\frac{150}{7}$,
誤差是|$\frac{150}{7}$-22|=$\frac{4}{7}$<1,
x=6時,$\widehat{y}$=$\frac{78}{7}$,誤差是|$\frac{78}{7}$-12|=$\frac{6}{7}$<1,
故該小組所得線性回歸方程是理想的.
點評 本題考查了求回歸方程問題,考查殘差的計算,是一道基礎題.


科目:高中數學 來源: 題型:選擇題

| A. | f(x)的圖象關于直線x=-$\frac{2π}{3}$對稱 | |
| B. | 函數f(x)在[-$\frac{π}{3}$,0]上單調遞增 | |
| C. | f(x)的圖象關于點(-$\frac{5π}{12}$,0)對稱 | |
| D. | 將函數y=2sin(2x-$\frac{π}{6}$)的圖象向左平移$\frac{π}{6}$個單位得到f(x)的圖象 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
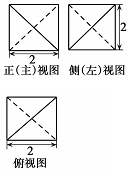
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com