
某企業生產甲、乙兩種產品,已知生產每噸甲產品要用 原料3噸,
原料3噸, 原料2噸;生產每噸乙產品要用
原料2噸;生產每噸乙產品要用 原料1噸,
原料1噸, 原料3噸.銷售每噸甲產品可獲得利潤4萬元、每噸乙產品可獲得利潤3萬元.該企業在一個生產周期內消耗
原料3噸.銷售每噸甲產品可獲得利潤4萬元、每噸乙產品可獲得利潤3萬元.該企業在一個生產周期內消耗 原料不超過13噸、
原料不超過13噸、 原料不超過18噸,那么該企業可獲得的最大利潤是 .
原料不超過18噸,那么該企業可獲得的最大利潤是 .
24萬元
解析試題分析:先設該企業生產甲產品為x噸,乙產品為y噸,列出約束條件,再根據約束條件畫出可行域,設z=6x+3y,再利用z的幾何意義求最值,只需求出直線z=4x+3y過可行域內的點時,從而得到z值即可.
根據題意得到不等式組為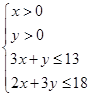 得到可行域如下圖所示
得到可行域如下圖所示
克制目標函數過可行域內的點M時,此時縱截距最大,由方程組 得到點M(3,4),故目標函數的最大值為12+12=24,即為24萬元。故答案為24萬元。
得到點M(3,4),故目標函數的最大值為12+12=24,即為24萬元。故答案為24萬元。
考點:本試題考查了線性規劃的知識點。
點評:在解決線性規劃的應用題時,其步驟為:①分析題目中相關量的關系,列出不等式組,即約束條件⇒②由約束條件畫出可行域⇒③分析目標函數Z與直線截距之間的關系⇒④使用平移直線法求出最優解⇒⑤還原到現實問題中.


 備戰中考寒假系列答案
備戰中考寒假系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com