
【題目】已知函數f(x)=ex﹣x2+2a+b(x∈R)的圖象在x=0處的切線為y=bx.(e為自然對數的底數).
(Ⅰ)求a,b的值;
(Ⅱ)若k∈Z,且f(x)+ ![]() (3x2﹣5x﹣2k)≥0對任意x∈R恒成立,求k的最大值.
(3x2﹣5x﹣2k)≥0對任意x∈R恒成立,求k的最大值.
【答案】解:(I)f′(x)=ex﹣2x,f′(0)=1=b,f(0)=1+2a+b=0,
聯立解得b=1,a=﹣1.
(II)由(I)可得:f(x)=e2﹣x2﹣1.
f(x)+ ![]() (3x2﹣5x﹣2k)≥0對任意x∈R恒成立k≤ex+
(3x2﹣5x﹣2k)≥0對任意x∈R恒成立k≤ex+ ![]() ﹣
﹣ ![]() x﹣1對x∈R恒成立.
x﹣1對x∈R恒成立.
令h(x)=ex+ ![]() ﹣
﹣ ![]() x﹣1,h′(x)=ex+x﹣
x﹣1,h′(x)=ex+x﹣ ![]() ,h″(x)=ex+1>0恒成立.
,h″(x)=ex+1>0恒成立.
∴h′(x)在R上單調遞增.
h′(0)= ![]() <0,h′(1)=
<0,h′(1)= ![]() >0,
>0, ![]() =
= ![]() <0,
<0, ![]() =
= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =0.
=0.
∴存在唯一零點x0∈ ![]() ,使得h′(x0)=0,
,使得h′(x0)=0,
當x∈(﹣∞,x0)時,h′(x0)<0,函數h(x)在(﹣∞,x0)單調遞減;當x∈(x0,+∞)時,h′(x0)>0,函數h(x)在(x0,+∞)上單調遞增.
∴h(x)min=h(x0)= ![]() +
+ ![]() ﹣
﹣ ![]() ﹣1,又h′(x0)=
﹣1,又h′(x0)= ![]() +x0﹣
+x0﹣ ![]() =0,∴
=0,∴ ![]() =
= ![]() ﹣x0,
﹣x0,
∴h(x0)= ![]() ﹣x0+
﹣x0+ ![]() ﹣
﹣ ![]() ﹣1=
﹣1= ![]() ,
,
∵x0∈ ![]() ,∴h(x0)∈
,∴h(x0)∈ ![]() .
.
又k≤ex+ ![]() ﹣
﹣ ![]() x﹣1對x∈R恒成立k≤h(x0),k∈Z.
x﹣1對x∈R恒成立k≤h(x0),k∈Z.
∴k的最大值為﹣1
【解析】(I)f′(x)=ex﹣2x,f′(0)=1=b,f(0)=1+2a+b=0,聯立解得b,a.(II)由(I)可得:f(x)=e2﹣x2﹣1.f(x)+ ![]() (3x2﹣5x﹣2k)≥0對任意x∈R恒成立k≤ex+
(3x2﹣5x﹣2k)≥0對任意x∈R恒成立k≤ex+ ![]() ﹣
﹣ ![]() x﹣1對x∈R恒成立.令h(x)=ex+
x﹣1對x∈R恒成立.令h(x)=ex+ ![]() ﹣
﹣ ![]() x﹣1,h′(x)=ex+x﹣
x﹣1,h′(x)=ex+x﹣ ![]() ,h″(x)=ex+1>0恒成立.可得h′(x)在R上單調遞增.h′(0)<0,h′(1)>0,
,h″(x)=ex+1>0恒成立.可得h′(x)在R上單調遞增.h′(0)<0,h′(1)>0, ![]() <0,
<0, ![]() >0.可得存在唯一零點x0∈
>0.可得存在唯一零點x0∈ ![]() ,使得h′(x0)=0,利用單調性可得:h(x)min=h(x0)=
,使得h′(x0)=0,利用單調性可得:h(x)min=h(x0)= ![]() +
+ ![]() ﹣
﹣ ![]() ﹣1,進而得出結論.
﹣1,進而得出結論.


科目:高中數學 來源: 題型:
【題目】已知矩形ADEF和菱形ABCD所在平面互相垂直,如圖,其中AF=1,AD=2,∠ADC= ![]() ,點N時線段AD的中點.
,點N時線段AD的中點. 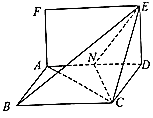
(Ⅰ)試問在線段BE上是否存在點M,使得直線AF∥平面MNC?若存在,請證明AF∥平面MNC,并求出 ![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(Ⅱ)求二面角N﹣CE﹣D的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期為π,且f(﹣x)=f(x),則( )
)的最小正周期為π,且f(﹣x)=f(x),則( )
A.f(x)在(0, ![]() )單調遞增
)單調遞增
B.f(x)在( ![]() ,
, ![]() )單調遞減
)單調遞減
C.f(x)在( ![]() ,
, ![]() )單調遞增
)單調遞增
D.f(x)在( ![]() ,π)單調遞增
,π)單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果存在常數a,使得數列{an}滿足:若x是數列{an}中的一項,則a﹣x也是數列{an}中的一項,稱數列{an}為“兌換數列”,常數a是它的“兌換系數”.
(1)若數列:2,3,6,m(m>6)是“兌換系數”為a的“兌換數列”,求m和a的值;
(2)已知有窮等差數列{bn}的項數是n0(n0≥3),所有項之和是B,求證:數列{bn}是“兌換數列”,并用n0和B表示它的“兌換系數”;
(3)對于一個不少于3項,且各項皆為正整數的遞增數列{cn},是否有可能它既是等比數列,又是“兌換數列”?給出你的結論,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,AC=BC=2,∠ACB=90°,側面PAB為等邊三角形,側棱 ![]() .
. 
(Ⅰ)求證:PC⊥AB;
(Ⅱ)求證:平面PAB⊥平面ABC;
(Ⅲ)求二面角B﹣AP﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人進行圍棋比賽,約定先連勝兩局者直接贏得比賽,若賽完 ![]() 局仍未出現連勝,則判定獲勝局數多者贏得比賽.假設每局甲獲勝的概率為
局仍未出現連勝,則判定獲勝局數多者贏得比賽.假設每局甲獲勝的概率為 ![]() ,乙獲勝的概率為
,乙獲勝的概率為 ![]() ,各局比賽結果相互獨立.
,各局比賽結果相互獨立.
(Ⅰ)求甲在4局以內(含 4 局)贏得比賽的概率;
(Ⅱ)記 X 為比賽決出勝負時的總局數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2013年至2016年期間,甲每年6月1日都到銀行存入m元的一年定期儲蓄,若年利率為q保持不變,且每年到期的存款本息自動轉為新的一年定期,到2017年6月1日甲去銀行不再存款,而是將所有存款的本息全部取回,則取回的金額是( )
A.m(1+q)4元
B.m(1+q)5元
C.![]() 元
元
D.![]() 元
元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() =(
=( ![]() sin
sin ![]() ,cos
,cos ![]() ,
, ![]() =(cos
=(cos ![]() ,cos
,cos ![]() ),f(x)=
),f(x)= ![]()
![]() .
.
(1)若函數f(x)的最小正周期和單調遞增區間;
(2)若a,b,c分別是△ABC的內角A,B,C所對的邊,且a=2,(2a﹣b)cosC=ccosB, ![]() ,求c.
,求c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x),g(x)分別是定義在R上的偶函數和奇函數,且f(x)+g(x)=2x , 若存在x0∈[1,2]使得等式af(x0)+g(2x0)=0成立,則實數a的取值范圍是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com