
【題目】(1)已知命題![]() :實數
:實數![]() 滿足
滿足![]() ,命題
,命題![]() :實數
:實數![]() 滿足方程
滿足方程![]() 表示的焦點在
表示的焦點在![]() 軸上的橢圓,且
軸上的橢圓,且![]() 是
是![]() 的充分不必要條件,求實數
的充分不必要條件,求實數![]() 的取值范圍;
的取值范圍;
(2)設命題![]() :關于
:關于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函數
:函數![]() 的定義域為
的定義域為![]() .若
.若![]() 是真命題,
是真命題,![]() 是假命題,求實數
是假命題,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)利用一元二次不等式的解法化簡![]() ,利用橢圓的標準方程化簡
,利用橢圓的標準方程化簡![]() ,由包含關系列不等式求解即可;(2)化簡命題
,由包含關系列不等式求解即可;(2)化簡命題![]() 可得
可得![]() ,化簡命題
,化簡命題![]() 可得
可得![]() ,由
,由![]() 為真命題,
為真命題,![]() 為假命題,可得
為假命題,可得![]() 一真一假,分兩種情況討論,對于
一真一假,分兩種情況討論,對于![]() 真
真![]() 假以及
假以及![]() 假
假![]() 真分別列不等式組,分別解不等式組,然后求并集即可求得實數
真分別列不等式組,分別解不等式組,然后求并集即可求得實數![]() 的取值范圍.
的取值范圍.
詳解:(1)由![]() 得:
得:![]() ,即命題
,即命題![]()
由![]() 表示焦點在
表示焦點在![]() 軸上的橢圓,可得
軸上的橢圓,可得![]() ,解得
,解得![]() ,即命題
,即命題![]() .
.
因為![]() 是
是![]() 的充分不必要條件,所以
的充分不必要條件,所以 或
或
解得:![]() ,∴實數
,∴實數![]() 的取值范圍是
的取值范圍是![]() .
.
(2)解:命題![]() 為真命題時,實數
為真命題時,實數![]() 的取值集合為
的取值集合為![]()
對于命題![]() :函數
:函數![]() 的定義域為
的定義域為![]() 的充要條件是
的充要條件是![]() ①恒成立.
①恒成立.
當![]() 時,不等式①為
時,不等式①為![]() ,顯然不成立;
,顯然不成立;
當![]() 時,不等式①恒成立的條件是
時,不等式①恒成立的條件是![]() ,解得
,解得![]()
所以命題![]() 為真命題時,
為真命題時,![]() 的取值集合為
的取值集合為![]()
由“![]() 是真命題,
是真命題,![]() 是假命題”,可知命題
是假命題”,可知命題![]() 、
、![]() 一真一假
一真一假
當![]() 真
真![]() 假時,
假時,![]() 的取值范圍是
的取值范圍是![]()
當![]() 假
假![]() 真時,
真時,![]()
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.


 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:
【題目】從某企業生產的產品中抽取100件,測量這些產品的一項質量指標值,由測量結果得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(1)在表格中作出這些數據的頻率分布直方圖;
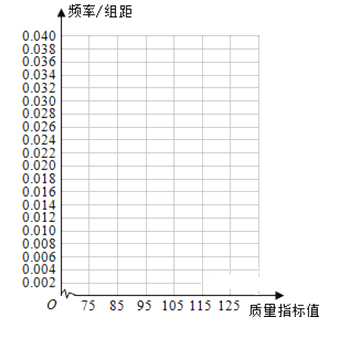
(2)求這些數據的眾數和中位數
(3)估計這種產品質量指標的平均數(同一組中的數據用該組區間的中點值作代表);
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)與g(x)是定義在同一區間[a,b]上的兩個函數,若函數y=f(x)﹣g(x)在x∈[a,b]上有兩個不同的零點,則稱f(x)和g(x)在[a,b]上是“關聯函數”,區間[a,b]稱為“關聯區間”.若f(x)=x2﹣3x+4與g(x)=2x+m在[0,3]上是“關聯函數”,則m的取值范圍 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學典籍《九章算術》“盈不足”中有一道兩鼠穿墻問題:“今有垣厚十尺,兩鼠對穿,初日各一尺,大鼠日自倍,小鼠日自半,問幾何日相逢?”現用程序框圖描述,如圖所示,則輸出結果n=( ) 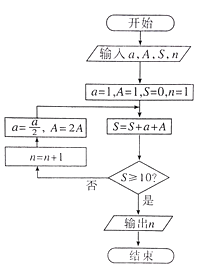
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為4的正方形,
是邊長為4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上一點,求三棱錐
上一點,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著蘋果6手機的上市,很多消費者覺得價格偏高,尤其是一部分大學生可望而不可及,因此“國美在線”推出無抵押分期付款購買方式,某分期店對最近100位采用分期付款的購買者進行統計,統計結果如下表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
頻 數 | 35 | 25 | a | 10 | b |
已知分3期付款的頻率為0.15,并且店銷售一部蘋果6,顧客分1期付款,其利潤為1千元;分2期或3期付款,其利潤為1.5千元;分4期或5期付款,其利潤為2千元,以頻率作為概率.
(1)求事件A:“購買的3位顧客中,至多有1位分4期付款”的概率;
(2)用X表示銷售一該手機的利潤,求X的分布列及數學期望E(x)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的焦距為
的焦距為![]() ,離心率為
,離心率為![]() ,橢圓的右頂點為
,橢圓的右頂點為![]() .
.
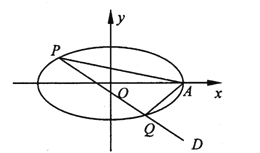
(1)求該橢圓的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓于兩個不同點
交橢圓于兩個不同點![]() ,求證:直線
,求證:直線![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解不等式![]() ;
;
(2)若函數![]() 在區間
在區間![]() 上存在零點,求實數
上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,其中
,其中![]() 為奇函數,
為奇函數,![]() 為偶函數,若不等式
為偶函數,若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com