
已知圓![]() :
:![]() 及定點
及定點![]() ,點
,點![]() 是圓
是圓![]() 上的動點,點
上的動點,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,且滿足
上,且滿足![]() =2
=2![]() ,
,
![]() ·
·![]() =
=![]() . (1)若
. (1)若![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若動圓![]() 和(1)中所求軌跡
和(1)中所求軌跡![]() 相交于不同兩點
相交于不同兩點![]() ,是否存在一組正實數
,是否存在一組正實數![]() ,使得直線
,使得直線![]() 垂直平分線段
垂直平分線段![]() ,若存在,求出這組正實數;若不存在,說明理由.
,若存在,求出這組正實數;若不存在,說明理由.
解:(1)![]() 點
點![]() 為
為![]() 的中點,
的中點,
又![]() ,
,
![]() 或
或![]() 點與
點與![]() 點重合.∴
點重合.∴![]() …………2分
…………2分
又![]()
∴點![]() 的軌跡是以
的軌跡是以![]() 為焦點的橢圓,
為焦點的橢圓,
且![]() ,
,
∴![]() 的軌跡方程是
的軌跡方程是![]() …………6分
…………6分
(2)
解:不存在這樣一組正實數,下面證明: ……7分
由題意,若存在這樣的一組正實數,當直線![]() 的斜率存在時,
的斜率存在時,
設之為![]() ,故直線
,故直線![]() 的方程為:
的方程為:
![]() ,設
,設![]() ,
,![]() 中點
中點![]() ,
,
則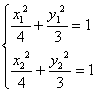 ,兩式相減得:
,兩式相減得:![]() .
.
…………9分
注意到![]() ,
,
且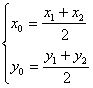 ,
,
則![]() , ②
, ②
又點![]() 在直線
在直線![]() 上,
上,![]() ,
,
代入②式得:![]() .
.
因為弦![]() 的中點
的中點![]() 在⑴所給橢圓
在⑴所給橢圓![]() 內,故
內,故![]() ,
,
這與![]() 矛盾,所以所求這組正實數不存在. …………13分
矛盾,所以所求這組正實數不存在. …………13分
當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() ,
,
則此時![]() ,
,
代入①式得![]() ,這與
,這與![]() 是不同兩點矛盾.
是不同兩點矛盾.
綜上,所求的這組正實數不存在. ………14分


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:高中數學 來源: 題型:
 如圖所示,已知圓M:(x+1)2+y2=8及定點N(1,0),點P是圓M上一動點,點Q為PN的中點,PM上一點G滿足
如圖所示,已知圓M:(x+1)2+y2=8及定點N(1,0),點P是圓M上一動點,點Q為PN的中點,PM上一點G滿足| GQ |
| NP |
查看答案和解析>>
科目:高中數學 來源:2011屆廣東省高三高考全真模擬試卷數學理卷二 題型:解答題
(本小題滿分14分)已知圓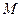 :
: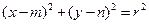 及定點
及定點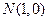 ,點
,點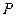 是圓
是圓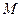 上的動點,點
上的動點,點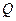 在
在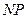 上,點
上,點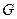 在
在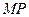 上,
上,
且滿足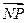 =2
=2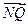 ,
,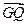 ·
·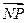 =
=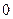 .
.
(1)若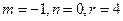 ,求點
,求點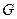 的軌跡
的軌跡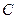 的方程;
的方程;
(2)若動圓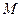 和(1)中所求軌跡
和(1)中所求軌跡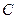 相交于不同兩點
相交于不同兩點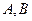 ,是否存在一組正實數
,是否存在一組正實數 ,使得直線
,使得直線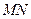 垂直平分線段
垂直平分線段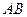 ,若存在,求出這組正實數;若不存在,說明理由.
,若存在,求出這組正實數;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年云南部分名校(玉溪一中)高三11月月考理科數學試卷(解析版) 題型:解答題
已知圓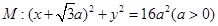 及定點
及定點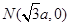 ,點
,點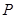 是圓
是圓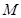 上的動點,點
上的動點,點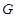 在
在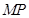 上,且滿足
上,且滿足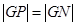 ,
,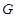 點的軌跡為曲線
點的軌跡為曲線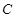 。
。
(1)求曲線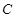 的方程;
的方程;
(2)若點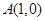 關于直線
關于直線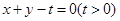 的對稱點在曲線
的對稱點在曲線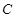 上,求
上,求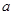 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知圓![]() :
:![]() 及定點
及定點![]() ,點
,點![]() 是圓
是圓![]() 上的動點,點
上的動點,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,且滿足
上,且滿足![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() .
.
(1)若![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若動圓![]() 和(1)中所求軌跡
和(1)中所求軌跡![]() 相交于不同兩點
相交于不同兩點![]() ,
,![]() 是否存在一組正實數
是否存在一組正實數![]() ,使得直線
,使得直線![]() 垂直平分線段
垂直平分線段![]() ,若存在,求出這組正實數;若不存在,說明理由.
,若存在,求出這組正實數;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com