
已知曲線 :
: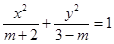
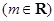 .
.
(1)若曲線 是焦點在
是焦點在 軸上的橢圓,求
軸上的橢圓,求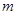 的取值范圍;
的取值范圍;
(2)設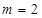 ,過點
,過點 的直線
的直線 與曲線
與曲線 交于
交于 ,
,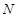 兩點,
兩點, 為坐標原點,若
為坐標原點,若 為直角,求直線
為直角,求直線 的斜率.
的斜率.
(1)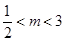 ;(2)
;(2) 的值為
的值為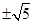 .
.
解析試題分析:(1)曲線 是焦點在
是焦點在 軸上的橢圓,則求解不等式組
軸上的橢圓,則求解不等式組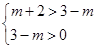 即可得到參數
即可得到參數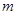 的取值范圍;(2)設
的取值范圍;(2)設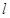 的方程為
的方程為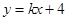 (注意檢驗斜率不存在的情況是否符合要求),再設出
(注意檢驗斜率不存在的情況是否符合要求),再設出 兩點的坐標
兩點的坐標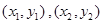 ,當
,當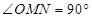 ,由
,由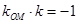 即
即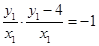 與
與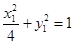 聯立可求解出點
聯立可求解出點 的坐標,然后再代入直線方程
的坐標,然后再代入直線方程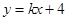 ,即可求出
,即可求出 的值.
的值.
試題解析:(1)若曲線 :
: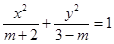 是焦點在
是焦點在 軸上的橢圓,則有
軸上的橢圓,則有
解得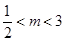 3分
3分
(2)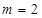 時,曲線
時,曲線 的方程為
的方程為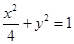 ,
, 為橢圓
為橢圓
由題意知,點 的直線
的直線 的斜率存在,所以設
的斜率存在,所以設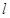 的方程為
的方程為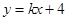
由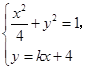 消去
消去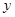 得
得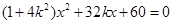 5分
5分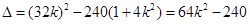 ,當
,當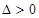 時,解得
時,解得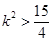
設 兩點的坐標分別為
兩點的坐標分別為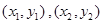
因為 為直角,所以
為直角,所以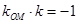 ,即
,即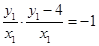
整理得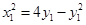 ① 7分
① 7分
又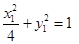 ,②將①代入②,消去
,②將①代入②,消去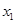 得
得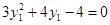
解得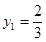 或
或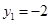 (舍去)
(舍去)
將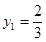 代入①,得
代入①,得 ,所以
,所以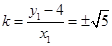
故所求 的值為
的值為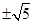 9分.
9分.
考點:1.橢圓的方程;2.直線與橢圓的位置關系;3.兩直線垂直的條件.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:解答題
設橢圓C: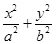 =1(a>b>0)的離心率e=
=1(a>b>0)的離心率e=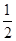 ,右焦點到直線
,右焦點到直線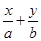 =1的距離d=
=1的距離d=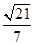 ,O為坐標原點.
,O為坐標原點.
(1)求橢圓C的方程;
(2)過點O作兩條互相垂直的射線,與橢圓C分別交于A,B兩點,證明,點O到直線AB的距離為定值,并求弦AB長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設點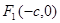 、
、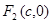 分別是橢圓
分別是橢圓 的左、右焦點,
的左、右焦點,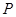 為橢圓
為橢圓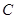 上任意一點,且
上任意一點,且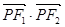 的最小值為
的最小值為 .
.
(I)求橢圓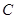 的方程;
的方程;
(II)設直線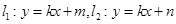 (直線
(直線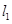 、
、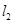 不重合),若
不重合),若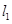 、
、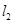 均與橢圓
均與橢圓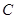 相切,試探究在
相切,試探究在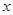 軸上是否存在定點
軸上是否存在定點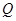 ,使點
,使點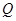 到
到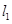 、
、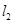 的距離之積恒為1?若存在,請求出點
的距離之積恒為1?若存在,請求出點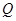 坐標;若不存在,請說明理由.
坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓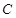 :
: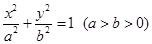 的左、右焦點分別為
的左、右焦點分別為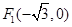 、
、 ,橢圓上的點
,橢圓上的點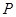 滿足
滿足 ,且△
,且△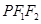 的面積為
的面積為 .
.
(Ⅰ)求橢圓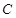 的方程;
的方程;
(Ⅱ)設橢圓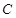 的左、右頂點分別為
的左、右頂點分別為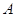 、
、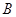 ,過點
,過點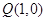 的動直線
的動直線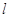 與橢圓
與橢圓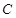 相交于
相交于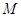 、
、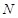 兩點,直線
兩點,直線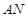 與直線
與直線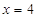 的交點為
的交點為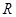 ,證明:點
,證明:點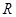 總在直線
總在直線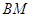 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知橢圓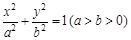 的右頂點為A(2,0),點P(2e,
的右頂點為A(2,0),點P(2e,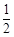 )在橢圓上(e為橢圓的離心率).
)在橢圓上(e為橢圓的離心率).
(1)求橢圓的方程;
(2)若點B,C(C在第一象限)都在橢圓上,滿足 ,且
,且 ,求實數λ的值.
,求實數λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在平面直角坐標系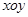 中,已知
中,已知 分別是橢圓
分別是橢圓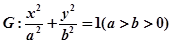 的左、右焦點,橢圓
的左、右焦點,橢圓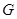 與拋物線
與拋物線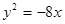 有一個公共的焦點,且過點
有一個公共的焦點,且過點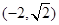 .
.
(Ⅰ)求橢圓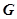 的方程;
的方程;
(Ⅱ)設直線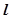 與橢圓
與橢圓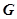 相交于
相交于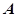 、
、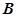 兩點,若
兩點,若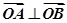 (
(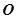 為坐標原點),試判斷直線
為坐標原點),試判斷直線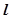 與圓
與圓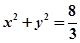 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知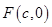 是橢圓
是橢圓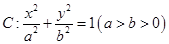 的右焦點;圓
的右焦點;圓 與
與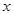 軸交于
軸交于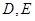 兩點,其中
兩點,其中 是橢圓
是橢圓 的左焦點.
的左焦點.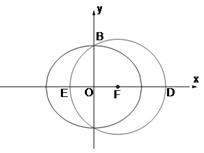
(1)求橢圓 的離心率;
的離心率;
(2)設圓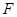 與
與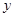 軸的正半軸的交點為
軸的正半軸的交點為 ,點
,點 是點
是點 關于
關于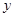 軸的對稱點,試判斷直線
軸的對稱點,試判斷直線 與圓
與圓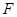 的位置關系;
的位置關系;
(3)設直線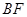 與圓
與圓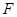 交于另一點
交于另一點 ,若
,若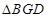 的面積為
的面積為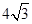 ,求橢圓
,求橢圓 的標準方程.
的標準方程.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(13分)如圖,某隧道設計為雙向四車道,車道總寬20m,要求通行車輛限高5m,隧道全長2.5km,隧道的兩側是與地面垂直的墻,高度為3米,隧道上部拱線近似地看成半個橢圓。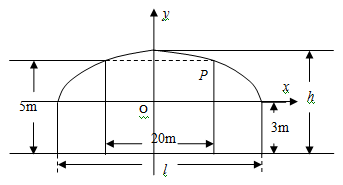
(1)若最大拱高h為6 m,則隧道設計的拱寬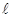 是多少?
是多少?
(2)若要使隧道上方半橢圓部分的土方工程 量最小,則應如何設計拱高h和拱寬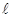 ?(已知:橢圓
?(已知:橢圓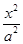 +
+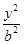 =1的面積公式為S=
=1的面積公式為S=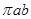 ,柱體體積為底面積乘以高。)
,柱體體積為底面積乘以高。)
(3)為了使隧道內部美觀,要求在拱線上找兩個點M、N,使它們所在位置的高度恰好是限高5m,現以M、N以及橢圓的左、右頂點為支點,用合金鋼板把隧道拱線部分連接封閉,形成一個梯形,若l=30m,梯形兩腰所在側面單位面積的鋼板造價是梯形頂部單位面積鋼板造價的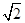 倍,試確定M、N的位置以及
倍,試確定M、N的位置以及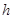 的值,使總造價最少。
的值,使總造價最少。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com