
已知:集合M是滿足下列性質的函數f(x)的全體:在定義域內存在x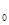 ,使得
,使得
f(x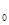 +1)=f(x
+1)=f(x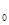 )+f(1)成立。
)+f(1)成立。
(1)函數f(x)=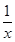 是否屬于集合M?說明理由;
是否屬于集合M?說明理由;
(2)設函數f(x)=lg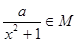 ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)證明:函數f(x)=2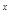 +x
+x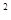
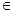 M。
M。
解:(Ⅰ)f(x)=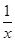 的定義域為
的定義域為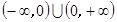 ,
,
令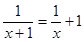 ,整理得x
,整理得x +x+1=0,△=-3<0,
+x+1=0,△=-3<0,
因此,不存在x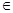
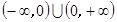 使得f(x+1)=f(x)+f(1)成立,所以f(x)=
使得f(x+1)=f(x)+f(1)成立,所以f(x)=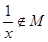 ; 3分
; 3分
(Ⅱ)f(x)=lg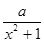 的定義域為R,f(1)=lg
的定義域為R,f(1)=lg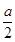 ,a>0,
,a>0,
若f(x)= lg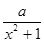
 M,則存在x
M,則存在x R使得lg
R使得lg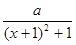 =lg
=lg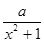 +lg
+lg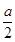 ,
,
整理得存在x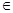 R使得(a
R使得(a -2a)x
-2a)x +2a
+2a x+(2a
x+(2a -2a)=0.
-2a)=0.
(1)若a -2a=0即a=2時,方程化為8x+4=0,解得x=-
-2a=0即a=2時,方程化為8x+4=0,解得x=-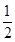 ,滿足條件:
,滿足條件:
(2)若a -2a
-2a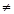 0即a
0即a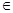
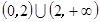 時,令△≥0,解得a
時,令△≥0,解得a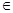
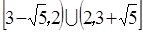 ,綜上,a
,綜上,a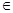 [3-
[3-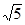 ,3+
,3+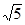 ];
7分
];
7分
(Ⅲ)f(x)=2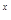 +x
+x 的定義域為R,
的定義域為R,
令2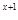 +(x+1)
+(x+1) =(2
=(2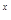 +x
+x )+(2+1),整理得2
)+(2+1),整理得2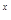 +2x-2=0,
+2x-2=0,
令g(x)=2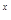 +2x-2,所以g(0)·g(1)=-2<0,
+2x-2,所以g(0)·g(1)=-2<0,
即存在x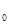
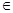 (0,1)使得g(x)=2
(0,1)使得g(x)=2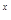 +2x-2=0,
+2x-2=0,
亦即存在x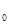
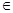 R使得2
R使得2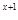 +(x+1)
+(x+1) =(2
=(2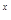 +x
+x )+(2+1),故f(x)=2
)+(2+1),故f(x)=2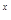 +x
+x
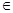 M。 10分
M。 10分
【解析】略


科目:高中數學 來源: 題型:
| 1 |
| x |
| a |
| x2+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| k | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:北京四中2011-2012學年高一上學期期中考試數學試題 題型:044
已知:集合M是滿足下列性質的函數f(x)的全體:在定義域內存在x0,使得![]() f(x0+1)=f(x0)+f(1)成立.
f(x0+1)=f(x0)+f(1)成立.
(1)函數f(x)=![]() 是否屬于集合M?說明理由;
是否屬于集合M?說明理由;
(2)設函數f(x)=lg![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)證明:函數f(x)=2x+x2∈M.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com