
已知數(shù)列 的前
的前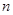 項和為
項和為 ,且
,且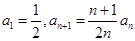 .
.
(1)求 的通項公式;
的通項公式;
(2)設(shè)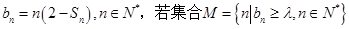 恰有5個元素,求實(shí)數(shù)
恰有5個元素,求實(shí)數(shù) 的取值范圍.
的取值范圍.
(1) ;(2)
;(2)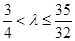 .
.
解析試題分析:(1)先將遞推式變形為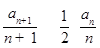 ,進(jìn)而判斷數(shù)列
,進(jìn)而判斷數(shù)列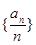 為等比數(shù)列,根據(jù)等比數(shù)列的通項公式即可求出
為等比數(shù)列,根據(jù)等比數(shù)列的通項公式即可求出 ;(2)由(1)中
;(2)由(1)中 ,該數(shù)列的通項是由一個等差與一個等比數(shù)列的通項公式相乘,于是可用錯位相減法求出
,該數(shù)列的通項是由一個等差與一個等比數(shù)列的通項公式相乘,于是可用錯位相減法求出 ,進(jìn)而得到
,進(jìn)而得到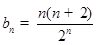 ,然后判斷數(shù)列
,然后判斷數(shù)列 的單調(diào)性,進(jìn)而根據(jù)集合
的單調(diào)性,進(jìn)而根據(jù)集合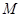 恰有5個元素,確定
恰有5個元素,確定 的取值范圍即可.
的取值范圍即可.
(1)由已知得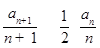 ,其中
,其中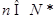
所以數(shù)列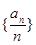 是公比為
是公比為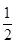 的等比數(shù)列,首項
的等比數(shù)列,首項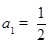
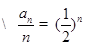 ,所以
,所以
由(1)知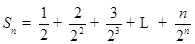
所以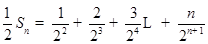
所以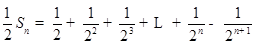
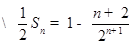
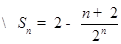
因此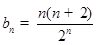 ,
,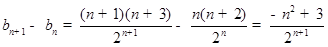
所以,當(dāng)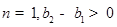 即
即 ,
,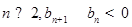 即
即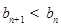

要使得集合 有5個元素,實(shí)數(shù)
有5個元素,實(shí)數(shù) 的取值范圍為
的取值范圍為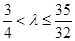 .
.
考點(diǎn):1.等比數(shù)列的通項公式;2.數(shù)列的前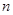 項和;3.數(shù)列的單調(diào)性.
項和;3.數(shù)列的單調(diào)性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列 的前
的前 項和為
項和為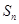 ,數(shù)列
,數(shù)列 是公比為
是公比為 的等比數(shù)列,
的等比數(shù)列, 是
是 和
和 的等比中項.
的等比中項.
(1)求數(shù)列 的通項公式;
的通項公式;
(2)求數(shù)列 的前
的前 項和
項和 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知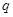 和
和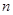 均為給定的大于1的自然數(shù).設(shè)集合
均為給定的大于1的自然數(shù).設(shè)集合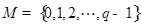 ,集合
,集合 .
.
(1)當(dāng)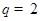 ,
,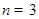 時,用列舉法表示集合
時,用列舉法表示集合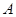 ;
;
(2)設(shè)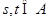 ,
,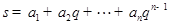 ,
,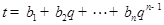 ,其中
,其中 證明:若
證明:若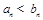 ,則
,則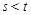 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知等比數(shù)列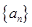 滿足:
滿足: ,公比
,公比 ,數(shù)列
,數(shù)列 的前
的前 項和為
項和為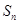 ,且
,且 .
.
(1)求數(shù)列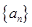 和數(shù)列
和數(shù)列 的通項
的通項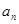 和
和 ;
;
(2)設(shè) ,證明:
,證明: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知數(shù)列 的各項均滿足
的各項均滿足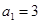 ,
, ,
,

(1)求數(shù)列 的通項公式;
的通項公式;
(2)設(shè)數(shù)列 的通項公式是
的通項公式是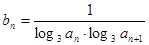 ,前
,前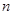 項和為
項和為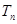 ,
,
求證:對于任意的正數(shù)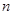 ,總有
,總有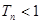 .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com