設函數f(x)=x2+bln(x+1),
(1)若對定義域的任意x,都有f(x)≥f(1)成立,求實數b的值;
(2)若函數f(x)在定義域上是單調函數,求實數b的取值范圍.
【答案】
分析:(1)根據對定義域的任意x,都有f(x)≥f(1)成立知函數f(x)在定義域內的最小值為f(1),從而得到f′(1)=0即可
(2)要求函數f(x)在定義域上是單調函數,即要求f′(x)≥0或f′(x)≤0在(-1,+∞)上恒成立,然后分類討論:當f′(x)≥0時,即2x
2+2x+b≥0在(-1,+∞)上恒成立,即b≥-2x
2-2x=
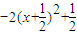
恒成立;當f′(x)≤0時,2x
2+2x+b≤0,即b≤-(2x
2+2x)恒成立,因-(2x
2+2x)在(-1,+∞)上沒有最小值,故不符合題意
解答:解:(1)由x+1>0得x>-1
∴f(x)的定義域為(-1,+∞),
對x∈(-1,+∞),都有f(x)≥f(1),
∴f(1)是函數f(x)的最小值,故有f′(1)=0,
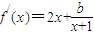
,∴
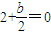
,
解得b=-4.
(2)∵
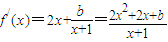
,
又函數f(x)在定義域上是單調函數,
∴f′(x)≥0或f′(x)≤0在(-1,+∞)上恒成立.
若f′(x)≥0,
∵x+1>0,
∴2x
2+2x+b≥0在(-1,+∞)上恒成立,
即b≥-2x
2-2x=
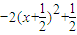
恒成立,由此得b≥

;
若f′(x)≤0,
∵x+1>0,
∴2x
2+2x+b≤0,即b≤-(2x
2+2x)恒成立,
因-(2x
2+2x)在(-1,+∞)上沒有最小值,
∴不存在實數b使f(x)≤0恒成立.
綜上所述,實數b的取值范圍是
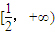
.
故答案為:(1)b=-4;(2)實數b的取值范圍是
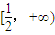
.
點評:本題考查了利用導數求閉區間上函數的最值,利用導數研究函數的單調性,另外還有分類討論的思想,屬于基礎題.

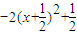 恒成立;當f′(x)≤0時,2x2+2x+b≤0,即b≤-(2x2+2x)恒成立,因-(2x2+2x)在(-1,+∞)上沒有最小值,故不符合題意
恒成立;當f′(x)≤0時,2x2+2x+b≤0,即b≤-(2x2+2x)恒成立,因-(2x2+2x)在(-1,+∞)上沒有最小值,故不符合題意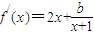 ,∴
,∴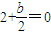 ,
,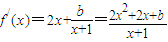 ,
,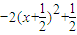 恒成立,由此得b≥
恒成立,由此得b≥ ;
;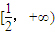 .
.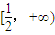 .
.

 寒假學與練系列答案
寒假學與練系列答案