Question

已知函數f（x）=ax﹣lnx+1（a∈R），g（x）=x e^1-x。
（1）求函數g（x）在區間（0，e]上的值域；
（2）是否存在實數a，對任意給定的x₀∈（0，e]，在區間[1，e]上都存在兩個不同的x_i（i=1，2），使得f（x_i）=g（x₀）成立，若存在，求出a的取值范圍；若不存在，請說明理由。
（3）給出如下定義：對于函數y=F（x）圖象上任意不同的兩點A（x₁，y₁），B（x₂，y₂），如果對于函數y=F（x）圖象上的點M（x₀，y₀）（其中總能使得F（x₁）﹣F（x₂）=F'（x₀）（x₁-x₂）成立，則稱函數具備性質“L”，試判斷函數f（x）是不是具備性質“L”，并說明理由。

Answer 1

解：（1）∵g'（x）=e^1-x+xe^1-x=e^x-1（1-x）在區間（0，1]上單調遞增，
在區間[1，e）上單調遞減，且g（0）=0，g（1）=1＞g（e）=e²-e
函數g（x）在區間（0，e]上的值域為（0，1]。
（2）令m=g（x），則由（1）可得m∈（0，1]，
原問題等價于：對任意的m∈（0，1]
f（x）=m在[1，e]上總有兩個不同的實根，
故f（x）在[1，e]不可能是單調函數                              
∴
當a≤0時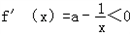，，在區間[1，e]上遞減，不合題意
當a≥1時，f'（x）＞0，在區間[1，e]上單調遞增，不合題意
當時，f'（x）＜0，在區間[1，e]上單調遞減，不合題意
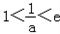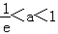當即時，在區間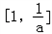上單調遞減；在區間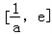上單遞增，
由上可得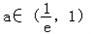，此時必有f（x）的最小值小于等于0且f（x）的最大值大于等于1，
而由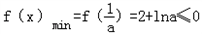可得，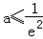
則a∈Φ
綜上，滿足條件的a不存在.
（3）設函數f（x）具備性質“L”，即在點M處地切線斜率等于k_AB，不妨設0＜x₁＜x₂，
則，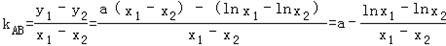
而f（x）在點M處的切線斜率為，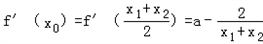
故有…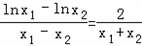
即，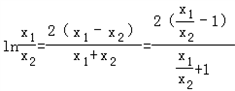
令，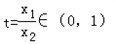
則上式化為，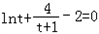
令F（t）=，
則由
可得F（t）在（0，1）上單調遞增，
故F（t）＜F（1）=0，
即方程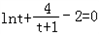無解，
所以函數f（x）不具備性質“L”。