廠家在產品出廠前,需對產品做檢驗,廠家將一批產品發給商家時,商家按合同規定需隨機抽取一定數量的產品做檢驗,以決定是否接收這批產品;
(1)若廠家庫房中的每件產品合格的概率為0.8,從中任意取出4件進行檢驗.求至少有1件是合格品的概率;
(2)若廠家發給商家20件產品,其中有3件不合格,商家從中任取2件進行檢驗,求該商家可能檢驗出不合格產品數X的分布列及均值EX;
(3)若廠家發給商家20件產品,其中有3件不合格,按合同規定該商家從發給的20件產品中任取2件,進行檢驗,只有2件都合格時才接收這批產品,否則拒收.,求該商家拒收這批產品的概率;
(以上問題的解答結果均用分數表示)
分析:(1)從中任意取出4件進行檢驗,至少有1件是合格品的對立事件是沒有合格品,根據相互獨立事件同時發生的概率做出沒有合格品的概率,再用對立事件的概率得到結果.
(2)該商家可能檢驗出不合格產品數X,X可能的取值為0,1,2,結合變量對應的事件,寫出變量對應的概率,寫出分布列,做出期望值.
(3)只有2件都合格時才接收這批產品,商家拒收這批產品的對立事件是商家任取2件產品檢驗都合格,先做出兩件產品都合格的概率,再用對立事件的概率公式得到結果.
解答:解:(1)從中任意取出4件進行檢驗,至少有1件是合格品的對立事件是沒有合格品,
記“廠家任取4件產品檢驗,其中至少有1件是合格品”為事件A,
用對立事件的概率公式有
P(A)=1-P()=1-0.24=.
(2)該商家可能檢驗出不合格產品數X,X可能的取值為0,1,2.
P(X=0)==,
P(X=1)==,
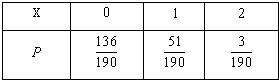 P(X=2)==
P(X=2)==.
EX=0×+1×+2×=(3)只有2件都合格時才接收這批產品,
商家拒收這批產品的對立事件是商家任取2件產品檢驗都合格,
記“商家任取2件產品檢驗都合格”為事件B,
則商家拒收這批產品的概率
P=1-P(B)=1-=,
∴商家拒收這批產品的概率為
.
點評:本題考查離散型隨機變量的分布列和期望,考查對立事件的概率,考查等可能事件的概率,求離散型隨機變量的分布列和期望是近年來理科高考必出的一個問題,題目做起來不難,運算量也不大,是一個好題.




![]() 的分布列及期望
的分布列及期望![]() ,并求該商家拒收這批產品的概率.
,并求該商家拒收這批產品的概率.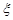 的分布列及期望
的分布列及期望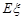 ,并求該商家拒收這批產品的概率.
,并求該商家拒收這批產品的概率.