
【題目】如圖,四棱錐P﹣ABCD的底面是邊長為a的正方形,PB⊥平面ABCD,M、N分別是AB、PC的中點. 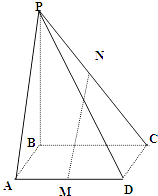
(1)求證:MN∥平面PAB;
(2)若平面PDA與平面ABCD成60°的二面角,求該四棱錐的體積.
【答案】
(1)證明:取PB的中點O,連接ON,OA,
∵O,N分別是PB,PC的中點,
∴ON∥BC,ON= ![]() BC
BC
又AD∥BC,AM= ![]() AD,
AD,
∴ON∥AM,ON=AM.
∴四邊形MNOA為平行四邊形.
∴MN∥AO
而MN平面PAB,AO平面PAB
∴MN∥平面PAB
(2)解:∵PB⊥平面ABCD,AD平面ABCD,
∴PB⊥AD,
又AB⊥AD,AB∩PB=B,
∴AD⊥面PAB,
∴AD⊥PA.
∴∠PAB為平面PDA與平面ABCD成二面角的平面角,
∴∠PAB=60°,
在RT△PBA中,PB=tan∠PABAB= ![]() a,
a,
∴VP﹣ABCD= ![]() SABCD×PB=
SABCD×PB= ![]() ×a2×
×a2× ![]() a=
a= ![]()
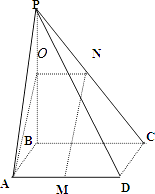
【解析】(1)取PB的中點O,連接ON,OA,通過證明四邊形MNOA為平行四邊形.得出MN∥AO,根據判定定理即可證明.(2)容易得出∠PAB為平面PDA與平面ABCD成二面角的平面角,在RT△PBA中,求出椎體的高PB,利用錐體體積公式計算即可.
【考點精析】解答此題的關鍵在于理解直線與平面平行的判定的相關知識,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,將曲線
中,將曲線![]() 上的所有點橫坐標伸長為原來的
上的所有點橫坐標伸長為原來的![]() 倍,縱坐標伸長為原來的2倍后,得到曲線
倍,縱坐標伸長為原來的2倍后,得到曲線![]() ,在以
,在以![]() 為極點,
為極點, ![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出曲線![]() 的參數方程和直線
的參數方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離
的距離![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,設動點M(2,t)(t>0).
(1)若過點P(0,4 ![]() )的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
)的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
(2)求以OM為直徑且被直線3x﹣4y﹣5=0截得的弦長為2的圓的方程;
(3)設A(1,0),過點A作OM的垂線與以OM為直徑的圓交于點N,求證:線段ON的長為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學一位高三班主任對本班50名學生學習積極性和對待班級工作的態度進行調查,得到的統計數據如表所示:
積極參加班級工作 | 不積極參加班級工作 | 合計 | |
學習積極性高 | 18 | 7 | 25 |
學習積極性不高 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機調查這個班的一名學生,那么抽到不積極參加班級工作且學習積極性不高的學生的概率是多少?
(2)若不積極參加班級工作且學習積極性高的7名學生中有兩名男生,現從中抽取2名學生參加某項活動,問2名學生中有1名男生的概率是多少?
(3)學生的學習積極性與對待班級工作的態度是否有關系?請說明理由.
附:

![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E,F,G,H分別為AA1 , AB,BB1 , B1C1的中點,則異面直線EF與GH所成的角等于 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a≠0,集合A={x|x2﹣x﹣6<0},B={x|x2+2x﹣8≥0},C={x|x2﹣4ax+3a2<0},且C(A∩RB).求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com