
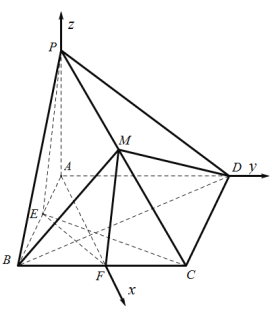
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,點
,點![]() 為棱
為棱![]() 的中點,點
的中點,點![]() 分別為棱
分別為棱![]() 上的動點(
上的動點(![]() 與所在棱的端點不重合),且滿足
與所在棱的端點不重合),且滿足![]() .
.
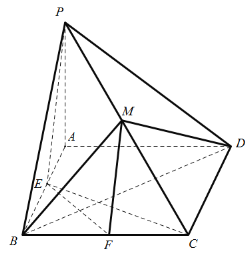
(1)證明:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)連接AC交BD于N,連接MN,證明MN∥PA,AC⊥MN得到AC⊥平面MBD,再根據EF∥AC得到證明.
(2)設BE=BF=x,由![]() ,得到E,F分別為棱AB,BC的中點時體積最大,以A為坐標原點,分別以AF,AD,AP所在直線為x,y,z軸建立空間直角坐標系,計算平面MEF和平面MEC的法向量,計算向量夾角得到答案.
,得到E,F分別為棱AB,BC的中點時體積最大,以A為坐標原點,分別以AF,AD,AP所在直線為x,y,z軸建立空間直角坐標系,計算平面MEF和平面MEC的法向量,計算向量夾角得到答案.
(1)連接AC交BD于N,連接MN,
∵底面ABCD為正方形,∴AC⊥BD,AN=NC,又∵PM=MC,∴MN∥PA,
由PA⊥底面ABCD知,MN⊥底面ABCD,又AC底面ABCD,∴AC⊥MN,
又BD∩MN=N,BD,MN平面MBD,∴AC⊥平面MBD,
在△ABC中,∵BE=BF,BA=BC,∴![]() ,即EF∥AC,
,即EF∥AC,
∴EF⊥平面MBD,又EF平面PEF,∴平面PEF⊥平面MBD;
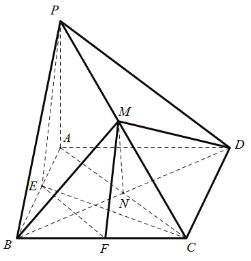
(2)設BE=BF=x,由題意![]() ,又PA=4,
,又PA=4,
∴![]() ,當x=2時,三棱錐F﹣PEC的體積最大.
,當x=2時,三棱錐F﹣PEC的體積最大.
即此時E,F分別為棱AB,BC的中點.
以A為坐標原點,分別以AF,AD,AP所在直線為x,y,z軸建立空間直角坐標系,
則C(![]() ,2,0),F(2
,2,0),F(2![]() ,0,0),E(
,0,0),E(![]() ,
,![]() ,0),M(
,0),M(![]() ,1,2),
,1,2),
![]() ,
,![]() ,
,![]() ,
,
設![]() ,
,
取![]() =1,得:
=1,得:![]() ,
,
設![]() 為平面MEC的一個法向量,則
為平面MEC的一個法向量,則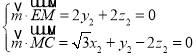 ,
,
取![]() =1,得:
=1,得:![]() ,則
,則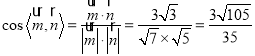 ,
,
由圖知所求二面角為銳二面角,所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
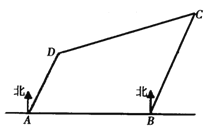
【題目】如圖,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正東方向,且與
的正東方向,且與![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏東
的北偏東![]() 方向,且與
方向,且與![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏東
的北偏東![]() 方向,且與
方向,且與![]() 相距
相距![]() ,一架飛機從城市
,一架飛機從城市![]() 出發以
出發以![]() 的速度向城市
的速度向城市![]() 飛行,飛行了
飛行,飛行了![]() ,接到命令改變航向,飛向城市
,接到命令改變航向,飛向城市![]() ,此時飛機距離城市
,此時飛機距離城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,點
的左、右焦點,點![]() 在橢圓上,且
在橢圓上,且![]() 軸,
軸,![]() 的周長為6.
的周長為6.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,設
兩點,設![]() 為坐標原點,是否存在常數
為坐標原點,是否存在常數![]() ,使得
,使得![]() 恒成立?請說明理由.
恒成立?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下面幾種說法:
①相等向量的坐標相同;
②若向量![]() 滿足
滿足![]() ,則
,則![]()
③若![]() ,
,![]() ,
,![]() ,
,![]() 是不共線的四點,則“
是不共線的四點,則“![]() ”是“四邊形
”是“四邊形![]() 為平行四邊形”的充要條件;
為平行四邊形”的充要條件;
④![]() 的充要條件是
的充要條件是![]() 且
且![]() .
.
其中正確說法的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
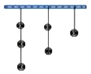
【題目】如圖所示,天花板上掛著3串玻璃球,射擊玻璃球規則:每次擊中1球,每串中下面球沒擊中,上面球不能擊中,則把這6個球全部擊中射擊方法數是( )
A.78B.60C.48D.36
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自出生之日起,人的情緒、體力、智力等心理、生理狀況就呈周期變化,變化由線為![]() .根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
.根據心理學家的統計,人體節律分為體力節律、情緒節律和智力節律三種.這些節律的時間周期分別為23天、28天、33天.每個節律周期又分為高潮期、臨界日和低潮期三個階段.以上三個節律周期的半數為臨界日,這就是說11.5天、14天、16.5天分別為體力節律、情緒節律和智力節律的臨界日.臨界日的前半期為高潮期,后半期為低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天計算).
(1)請寫出小英的體力、情緒和智力節律曲線的函數;
(2)試判斷小英在2019年4月22日三種節律各處于什么階段,當日小英是否適合參加某項體育競技比賽?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com