
分析 (1)利用指數函數的單調性,對底數a討論,即可單調性.
(2)令f(x)+g(x)-2=h(x).證明其奇偶性,利用奇偶性求值.
(3)利用(1)(2)中的結論,將不等式轉化為二次函數恒成立問題,即可求解t的取值范圍.
解答 解:(1)由題意:函數f(x)=$\frac{a}{{a}^{2}-1}$(a-x-ax),
①當0<a<1時,$f(x)=\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})$遞減,
②當a>1時,$f(x)=\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})$遞減,
∴當且a>0且a≠1時,f(x)是減函數.
(2)由題意g(x)=-ax+2.
設h(x)=f(x)+g(x)-2,則:h(x)=$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})-ax$,其定義域為R,關于原點對稱,
h(-x)=$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{-x}}-{a}^{-x})+ax$=$\frac{a}{{a}^{2}-1}({a}^{x}-\frac{1}{{a}^{x}})+ax$=-[$\frac{a}{{a}^{2}-1}(\frac{1}{{a}^{x}}-{a}^{x})-ax$]=-h(x)
∵h(-x)=-h(x),
∴h(x)是定義域為R的奇函數.
∵g(2)+f(2)=3,則:h(2)=1,
∴h(-2)=-1,即:g(2)+f(2)-2=-1
所以g(2)+f(2)=1.
(3)由(2)知h(x)是定義域為R的奇函數,且在R上為減函數,
由h(x2+tx)+h(4-x)<0,則有:h(x2+tx)<h(-4+x)
∴x2+tx>x-4,即x2+(t-1)x+4>0 恒成立,
∴△=b2-4ac=(t-1)2-16<0
解得:-3<t<5,
故得t的取值范圍是(-3,5).
點評 本題考查了復合函數的單調性和構造函數思想利用奇偶性求值,將恒等式問題轉化為不等式求解,綜合性強,屬于中檔題.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:選擇題
| A. | f(x)=x2+ax+1,a∈R | B. | f(x)=x+2a-1,a∈R | ||
| C. | f(x)=log2(ax2-1),a∈R | D. | f(x)=(x-a)|x|,a∈R |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
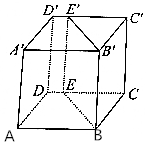 如圖,過正方體ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,則BB′與EE′的位置關系是( )
如圖,過正方體ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,則BB′與EE′的位置關系是( )| A. | 平行 | B. | 相交 | C. | 異面 | D. | 不確定 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1條 | B. | 2條 | C. | 3條 | D. | 4條 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com