
如圖,在三棱錐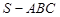 中,側面
中,側面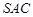 與底面
與底面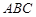 垂直,
垂直, 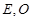 分別是
分別是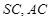 的中點,
的中點,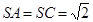 ,
,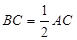 ,
,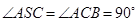 .
.
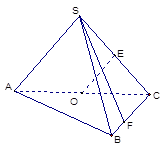
(1)若點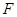 在線段
在線段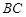 上,問:無論
上,問:無論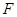 在
在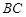 的何處,是否都有
的何處,是否都有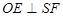 ?請證明你的結論;
?請證明你的結論;
(2)求二面角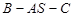 的平面角的余弦.
的平面角的余弦.
(1)詳見解析;(2)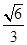
【解析】
試題分析:(1)考慮直線和直線垂直,只需考慮直線和平面垂直即可,由已知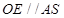 ,故可將
,故可將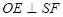 轉移到判斷
轉移到判斷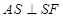 ,只需考慮
,只需考慮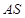 是否垂直于面
是否垂直于面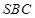 ,由已知得
,由已知得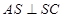 ,故只需說明
,故只需說明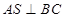 ,進而只需說明
,進而只需說明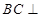 面
面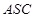 ,由已知側面
,由已知側面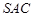 與底面
與底面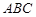 垂直,且
垂直,且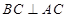 ,易證;(2)先將二面角
,易證;(2)先將二面角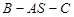 的平面角找到,再求,由(1)得
的平面角找到,再求,由(1)得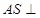 面
面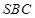 ,則
,則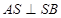 ,
,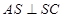 ,故
,故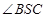 是所求的角,在
是所求的角,在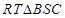 求解即可.
求解即可.
試題解析:(1)在△SAB中,∵OE∥AS,∠ASC=90°∴OE⊥SC
∵平面SAC⊥平面ABC,∠BCA=90°,∴BC⊥平面ASC,OE⊂平面ASC,
∴BC⊥OE∴OE⊥平面BSC,∵SF⊂平面BSC
∴OE⊥SF所以無論F在BC的何處,都有OE⊥SF
(2)由(1)BC⊥平面ASC∴BC⊥AS,又∵∠ASC=90°∴AS⊥SC
∴AS⊥平面BCS,∴AS⊥SB,∴∠BSC是二面角B-AS-C的平面角
在Rt△BCS中,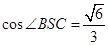
 ,所以二面角B-AS-C的平面角的余弦值為
,所以二面角B-AS-C的平面角的余弦值為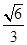 …
…
考點:1、直線和平面垂直的判定和性質;2、面面垂直的性質;3、二面角.


科目:高中數學 來源:2013-2014學年廣東省中山市實驗高中高三11月階段考試文科數學試卷(解析版) 題型:解答題
如圖,在三棱錐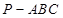 中,
中,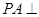 平面
平面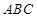 ,
,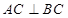 ,
,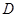 為側棱
為側棱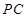 上一點,它的正(主)視圖和側(左)視圖如圖所示.
上一點,它的正(主)視圖和側(左)視圖如圖所示.
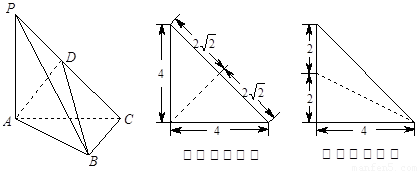
(1)證明: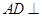 平面
平面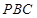 ;
;
(2)在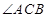 的平分線上確定一點
的平分線上確定一點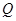 ,使得
,使得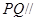 平面
平面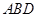 ,并求此時
,并求此時 的長.
的長.
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇省高三開學檢測理科數學試卷(解析版) 題型:解答題
如圖,在四棱錐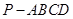 中,側棱
中,側棱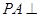 底面
底面 ,底面
,底面 為矩形,
為矩形,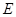 為
為 上一點,
上一點,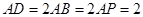 ,
,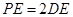 .
.
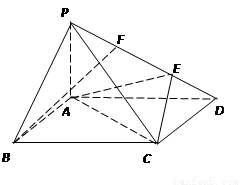
(I)若 為
為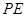 的中點,求證
的中點,求證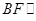 平面
平面 ;
;
(II)求三棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇省高三開學檢測文科數學試卷(解析版) 題型:解答題
如圖,在四棱錐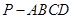 中,側棱
中,側棱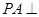 底面
底面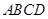 ,底面
,底面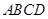 為矩形,
為矩形,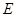 為
為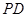 上一點,
上一點,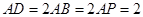 ,
,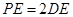 .
.
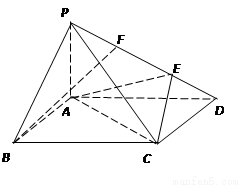
(I)若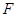 為
為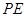 的中點,求證
的中點,求證 平面
平面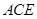 ;
;
(II)求三棱錐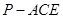 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年陜西省高三第六次適應性訓練文科數學(解析版) 題型:解答題
如圖,在三棱錐 中,
中, 平面
平面 ,
, ,
, 為側棱
為側棱 上一點,它的正(主)視圖和側(左)視圖如圖所示.
上一點,它的正(主)視圖和側(左)視圖如圖所示.
(1)證明: 平面
平面 ;
;
(2)求三棱錐 的體積;
的體積;
(3)在 的平分線上確定一點
的平分線上確定一點 ,使得
,使得 平面
平面 ,并求此時
,并求此時 的長.
的長.

查看答案和解析>>
科目:高中數學 來源:2010-2011學年北京市朝陽區高三上學期期末理科數學卷 題型:解答題
如圖,在三棱錐 中,
中, ,
, ,側面
,側面 為等邊三角形,側棱
為等邊三角形,側棱 .
.

(Ⅰ)求證: ;
;
(Ⅱ)求證:平面 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值
的余弦值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com