
【題目】若存在實常數k和b,使得函數F(x)和G(x)對其公共定義域上的任意實數x都滿足:F(x)≥kx+b和G(x)≤kx+b恒成立,則稱此直線y=kx+b為F(x)和G(x)的“隔離直線”,已知函數f(x)=x2(x∈R),g(x)= ![]() (x<0),h(x)=2elnx,有下列命題:
(x<0),h(x)=2elnx,有下列命題:
①F(x)=f(x)﹣g(x)在 ![]() 內單調遞增;
內單調遞增;
②f(x)和g(x)之間存在“隔離直線”,且b的最小值為﹣4;
③f(x)和g(x)之間存在“隔離直線”,且k的取值范圍是(﹣4,0];
④f(x)和h(x)之間存在唯一的“隔離直線”y=2 ![]() x﹣e.
x﹣e.
其中真命題的個數為(請填所有正確命題的序號)
【答案】①②④
【解析】解:①∵F(x)=f(x)﹣g(x)=x2﹣ ![]() ,∴x∈(﹣
,∴x∈(﹣ ![]() ,0),F′(x)=2x+
,0),F′(x)=2x+ ![]() >0,∴F(x)=f(x)﹣g(x)在x∈(﹣
>0,∴F(x)=f(x)﹣g(x)在x∈(﹣ ![]() ,0)內單調遞增,故①對;
,0)內單調遞增,故①對;
②、③設f(x)、g(x)的隔離直線為y=kx+b,則x2≥kx+b對一切實數x成立,即有△1≤0,k2+4b≤0,
又 ![]() ≤kx+b對一切x<0成立,則kx2+bx﹣1≤0,即△2≤0,b2+4k≤0,k≤0,b≤0,
≤kx+b對一切x<0成立,則kx2+bx﹣1≤0,即△2≤0,b2+4k≤0,k≤0,b≤0,
即有k2≤﹣4b且b2≤﹣4k,k4≤16b2≤﹣64k﹣4≤k≤0,同理﹣4≤b≤0,故②對,③錯;
④函數f(x)和h(x)的圖象在x= ![]() 處有公共點,因此存在f(x)和g(x)的隔離直線,
處有公共點,因此存在f(x)和g(x)的隔離直線,
那么該直線過這個公共點,設隔離直線的斜率為k.則隔離直線方程為y﹣e=k(x﹣ ![]() ),即y=kx﹣k
),即y=kx﹣k ![]() +e,
+e,
由f(x)≥kx﹣k ![]() +e(x∈R),可得x2﹣kx+k
+e(x∈R),可得x2﹣kx+k ![]() ﹣e≥0當x∈R恒成立,
﹣e≥0當x∈R恒成立,
則△≤0,只有k=2 ![]() ,此時直線方程為:y=2
,此時直線方程為:y=2 ![]() x﹣e,
x﹣e,
下面證明h(x)≤2 ![]() x﹣e,令G(x)=2
x﹣e,令G(x)=2 ![]() x﹣e﹣h(x)=2
x﹣e﹣h(x)=2 ![]() x﹣e﹣2elnx,
x﹣e﹣2elnx,
G′(x)= 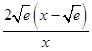 ,
,
當x= ![]() 時,G′(x)=0,當0<x<
時,G′(x)=0,當0<x< ![]() 時,G′(x)<0,當x>
時,G′(x)<0,當x> ![]() 時,G′(x)>0,
時,G′(x)>0,
則當x= ![]() 時,G(x)取到極小值,極小值是0,也是最小值.
時,G(x)取到極小值,極小值是0,也是最小值.
所以G(x)=2 ![]() x﹣e﹣g(x)≥0,則g(x)≤2
x﹣e﹣g(x)≥0,則g(x)≤2 ![]() x﹣e當x>0時恒成立.
x﹣e當x>0時恒成立.
∴函數f(x)和g(x)存在唯一的隔離直線y=2 ![]() x﹣e,故④正確.
x﹣e,故④正確.
所以答案是:①②④.
【考點精析】本題主要考查了命題的真假斷與應用的相關知識點,需要掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系才能正確解答此題.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}是各項均為正數的等差數列,其中a1=1,且a2、a4、a6+2成等比數列;數列{bn}的前n項和為Sn , 滿足2Sn+bn=1
(1)求數列{an}、{bn}的通項公式;
(2)如果cn=anbn , 設數列{cn}的前n項和為Tn , 求證:Tn<Sn+ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,A={y|y=2x+1},B={x|lnx<0},則(UA)∩B=( )
A.?
B.{x| ![]() <x≤1}
<x≤1}
C.{x|x<1}
D.{x|0<x<1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=sin(2014x+ ![]() )+cos(2014x﹣
)+cos(2014x﹣ ![]() )的最大值為A,若存在實數x1 , x2 , 使得對任意實數x總有f(x1)≤f(x)≤f(x2)成立,則A|x1﹣x2|的最小值為( )
)的最大值為A,若存在實數x1 , x2 , 使得對任意實數x總有f(x1)≤f(x)≤f(x2)成立,則A|x1﹣x2|的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,直線PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
(I)求證:直線DE⊥平面PAC.
(Ⅱ)若直線PE與平面PAC所成的角的正弦值為 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.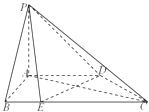
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+ ![]()
(1)若函數有兩個極值點,求實數a的取值范圍;
(2)對所有的a≥ ![]() ,m∈(0,1),n∈(1,+∞),求f(n)﹣f(m)的最小值.
,m∈(0,1),n∈(1,+∞),求f(n)﹣f(m)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=ax2+bx+c的圖象與x軸有兩個不同的交點,若f(c)=0且0<x<c時,f(x)>0,
(1)證明:![]() 是f(x)=0的一個根;
是f(x)=0的一個根;
(2)試比較![]() 與c的大小;
與c的大小;
(3)證明:-2<b<-1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com