

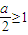
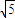 ,且△DNM∽△DAP
,且△DNM∽△DAP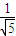 ,
,
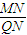 =
=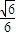


科目:高中數學 來源: 題型:
 ,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.
,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD,且PA=1.查看答案和解析>>
科目:高中數學 來源:2014屆吉林省高二4月月考理科數學試卷(解析版) 題型:解答題
如圖所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.


(1)試建立適當的坐標系,并寫出點P、B、D的坐標;
(2)問當實數a在什么范圍時,BC邊上能存在點Q,使得PQ⊥QD?
(3)當BC邊上有且僅有一個點Q使得PQ⊥QD時,求二面角Q-PD-A的大小.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年海南省國興中學、海師附中、嘉積中學、三亞一中高三聯考數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com