Question

已知斜三棱柱ABC-A₁B₁C₁的側(cè)面AA₁C₁C是面積為

3

2

的菱形，∠AA₁C₁為銳角，側(cè)面ABB₁A₁⊥AA₁C₁C，且A₁B=AB=AC=1．
（Ⅰ）求證：AA₁⊥BC₁；
（Ⅱ）求A₁到平面ABC的距離；
（Ⅲ）求二面角B-AC-C₁的余弦值．

Answer 1

分析：（Ⅰ）要證：AA₁⊥BC₁，先說明△AA₁B是等邊三角形，設(shè)D是AA₁的中點(diǎn)、連接BD，C₁D，證明AA₁⊥平面BC₁D，即可．
（Ⅱ）根據(jù)上一問得到的結(jié)論，OA、OC₁、OB兩兩垂直以O(shè)為原點(diǎn)，建立如圖空間直角坐標(biāo)系，寫出要用的點(diǎn)的坐標(biāo)，和向量的坐標(biāo)，根據(jù)點(diǎn)到平面的距離公式得到結(jié)果．
（Ⅲ）根據(jù)上一問做出的平面的法向量，和另一個(gè)平面的在圖形中存在的法向量，用兩個(gè)法向量所成的角，得到兩個(gè)平面之間的夾角的余弦．

解答：解：（Ⅰ）證明：因?yàn)樗倪呅蜛A₁C₁C是菱形，所以有AA₁=A₁C₁=C₁C=CA=1．
從而知△AA₁B是等邊三角形．（2分）
設(shè)D是AA₁的中點(diǎn)、連接BD，C₁D，
則BD⊥AA₁，由 S菱形A A1C1C =

3

2

．
知C₁到AA₁的距離為

3

2

．∠AA₁C₁=60°，
所以△AA₁C₁是等邊三角形，（4分）
且C₁D⊥AA₁，所以AA₁⊥平面BC₁D．（6分）
又BC₁?平面BC₁D，故AA₁⊥BC₁．（7分）

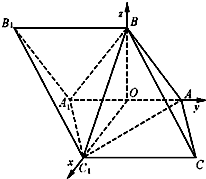
（Ⅱ）由（Ⅰ）知C₁O⊥AA₁，BO⊥AA₁
∵平面ABB₁A₁⊥平面AA₁C₁C，
∴BO⊥平面AA₁C₁C，C₁O?平面AA₁C₁C
BO⊥C₁O
∴OA、OC₁、OB兩兩垂直，…（6分）
以O(shè)為原點(diǎn)，建立如圖空間直角坐標(biāo)系，則：
O（0，0，0），A（0，

1

2

，0），A₁（0，-

1

2

，0），B（0，0，

3

2

），C1(

3

2

，0，0)．…（7分）
設(shè)

n

=(x，y．z)
是平面ABC的一個(gè)法向量，
則-

1

2

y+

3

2

z=0，

3

2

x+

1

2

y=0
令z=1，則

n

=(-1，

3

，1)．    …（9分）
設(shè)A1到平面ABC的距離為d．

AA1

=(0，-1，0)，
∴d=

| AA1 • n  |

| n |

=

15

5

．     …（10分）
（Ⅲ）由（Ⅱ）知平面ABC的一個(gè)法向量是

n

=(-1，

3

，1)．，…（11分）
又平面ACC₁的一個(gè)法向量

OB

=（0，0，

3

2

）．          …（12分）
∴cosθ=

OB • n

| OB || n |

=

3 2

5 × 3 2

=

5

5

．          …（13分）
∴二面角B-AC-C₁的余弦值是

5

5

．               …（14分）

點(diǎn)評(píng)：本題考查直線與平面的垂直，考查空間想象能力，邏輯思維能力，考查用空間向量來解決立體幾何距離和面面之間的夾角的問題，是中檔題．