
在三棱錐 中,
中, 兩兩垂直,且
兩兩垂直,且 ,
, ,
, ,則點
,則點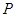 到
到 的重心
的重心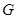 的距離為 .
的距離為 .
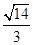
【解析】
試題分析:以PA、PB、PC為過同一頂點的三條棱,構造長方體,以CP為x軸,以CD為y軸,以CG為z軸,建立空間直角坐標系,利用向量法求解.根據題意,
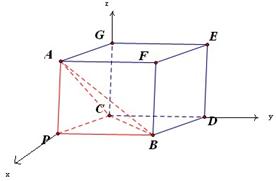
解:以PA、PB、PC為過同一頂點的三條棱,作長方體如圖,以CP為x軸,以CD為y軸,以CG為z軸,建立空間直角坐標系,∵PA=1,PB=2,PC=3,∴P(3,0,0),A(3,0,1),B(2,3,0),C(0,0,0),根據平面的法向量來得到點P到平平面的距離,然后根據重心的位置,結合勾股定理來得到點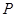 到
到 的重心
的重心 的距離為
的距離為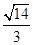 。故答案為
。故答案為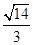
考點:點到面的距離的運用
點評:本題考查點到平面的距離的求法,解題時要認真審題,合理地構造長方體,注意向量法的合理運用.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源:2013-2014學年湖北穩派教育高三上學期強化訓練(三)理科數學試卷(解析版) 題型:選擇題
在三棱錐 中,
中, 兩兩垂直,且
兩兩垂直,且 ,設
,設 是底面
是底面 內一點,定義
內一點,定義 ,其中
,其中 分別是三棱錐
分別是三棱錐 ,三棱錐
,三棱錐 ,三棱錐
,三棱錐 的體積,若
的體積,若 ,且
,且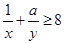 ,則正實數
,則正實數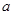 的最小值為( )
的最小值為( )
A.  B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源:2014屆重慶市高二4月月考理科數學試卷(解析版) 題型:填空題
如圖,在三棱錐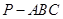 中,
中,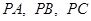 兩兩垂直,且
兩兩垂直,且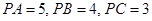 .設點
.設點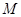 為底面
為底面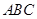 內一點,定義
內一點,定義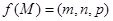 ,其中
,其中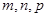 分別為三棱錐
分別為三棱錐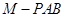 、
、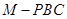 、
、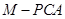 的體積.若
的體積.若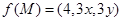 ,且
,且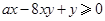 恒成立,則正實數
恒成立,則正實數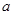 的取值范圍是___________.
的取值范圍是___________.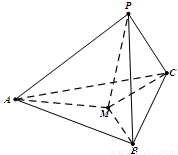
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省臺州市高三上學期期末理科數學試卷 題型:解答題
如圖,在三棱錐 中,
中, 兩兩垂直且相等,過
兩兩垂直且相等,過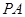 的中點
的中點 作平面
作平面 ∥
∥ ,且
,且 分別交
分別交 于
于 ,交
,交 的延長線于
的延長線于 .
.
(Ⅰ)求證: 平面
平面 ;
;
(Ⅱ)若 ,求二面角
,求二面角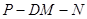 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
在三棱錐![]() 中,
中,![]() 兩兩互相垂直,
兩兩互相垂直,![]() .點
.點![]() 分別在側面
分別在側面![]() ,棱
,棱![]() 上運動。
上運動。![]() ,
,![]() 為線段
為線段![]() 的中點,當
的中點,當![]() 運動時,點
運動時,點![]() 的軌跡把三棱錐
的軌跡把三棱錐![]() 分成兩部分的體積之比等于 ( )
分成兩部分的體積之比等于 ( )
A.1:63 B.1:(16![]() ) C.
) C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com