已知函數f(x)=x3+ax2+3bx+c(b≠0),且g(x)=f(x)-2是奇函數.
(Ⅰ)求a,c的值;
(Ⅱ)求函數f(x)的單調區間.
【答案】
分析:(1)先利用奇函數的定義g(-x)=-g(x)求出a,c的值;
(2)求導數令其為0,判斷根左右兩邊的符號,求出函數的單調性.注意對參數的討論.
解答:解:(Ⅰ)因為函數g(x)=f(x)-2為奇函數,
所以,對任意的x∈R,都有g(-x)=-g(x),即f(-x)-2=-f(x)+2.
又f(x)=x
3+ax
2+3bx+c
所以-x
3+ax
2-3bx+c-2=-x
3-ax
2-3bx-c+2.
所以
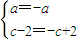
解得a=0,c=2.
(Ⅱ)由(Ⅰ)得f(x)=x
3+3bx+2.
所以f'(x)=3x
2+3b(b≠0).
當b<0時,由f'(x)=0得

.x變化時,f'(x)的變化情況如下:
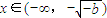
,時f′(x)>0
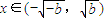
,時f′(x)<0
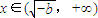
,時f′(x)>0
所以,當b<0時,函數f(x)在
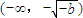
上單調遞增,
在
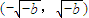
上單調遞減,在
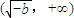
上單調遞增.
當b>0時,f'(x)>0,所以函數f(x)在(-∞,+∞)上單調遞增.
點評:本題考查函數的奇偶性,利用導數求函數的單調區間的方法.注意:含參數的函數求單調性時一般需要討論.

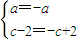
 .x變化時,f'(x)的變化情況如下:
.x變化時,f'(x)的變化情況如下: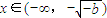 ,時f′(x)>0
,時f′(x)>0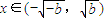 ,時f′(x)<0
,時f′(x)<0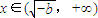 ,時f′(x)>0
,時f′(x)>0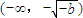 上單調遞增,
上單調遞增,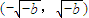 上單調遞減,在
上單調遞減,在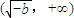 上單調遞增.
上單調遞增.

 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<