分析:由題意得:曲線
(θ為參數),表示圓心在A(2,0),半徑為1的圓,此圓上一點P(x,y)到點Q(5,-4)的距離的最大值的平方即為(x-5)
2+(y+4)
2的最大值,再利用圖形得出,圓上一點P(x,y)到點Q(5,-4)的距離的最大值等于此點到圓心的距離加上半徑,從而得出(x-5)
2+(y+4)
2的最大值.
解答: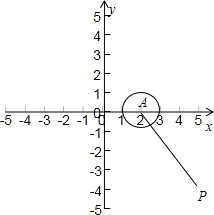
解:由題意得:曲線
(θ為參數),消去參數θ得:
(x-2)
2+y
2=1表示圓心在A(2,0),半徑為1的圓,
此圓上一點P(x,y)到點Q(5,-4)的距離的最大值的平方即為(x-5)
2+(y+4)
2的最大值,
由圖得,圓上一點P(x,y)到點Q(5,-4)的距離的最大值等于:
AQ+1=
+1=5+1=6則(x-5)
2+(y+4)
2的最大值為36.
故選C.
點評:本小題主要考查圓的參數方程、點到直線的距離公式等基礎知識,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于基礎題.

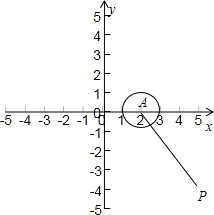 解:由題意得:曲線
解:由題意得:曲線
