Question

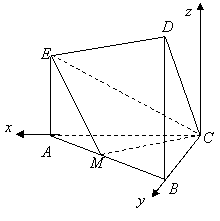
（07年浙江卷理）（14分）在如圖所示的幾何體中，平面，平面，，且，是的中點．

（I）求證：；

（II）求與平面所成的角．

Answer 1

本題主要考查空間線面關系、空間向量的概念與運算等基礎知識，同時考查空間想象能力和推理運算能力．

解析：方法一：

（I）證明：因為，是的中點，

所以．

又平面，

所以．

（II）過點作平面，垂足是，連結交延長交于點，連結，．是直線和平面所成的角．

因為平面，

所以，

又因為平面，

所以，

則平面，因此．

設，，

在直角梯形中，

，是的中點，

所以，，，

得是直角三角形，其中，

所以．

在中，，

所以，

故與平面所成的角是．

方法二：

如圖，以點為坐標原點，以，分別為軸和軸，過點作與平面垂直的

直線為軸，建立直角坐標系，

設，則，，

．，．

（I）證明：因為，，

所以，

故．

（II）設向量與平面垂直，則，，

即，．

因為，，

所以，，

即，

，

直線與平面所成的角是與夾角的余角，

所以，

因此直線與平面所成的角是．