
如圖,小島A在港口P的南偏西60°方向,距離港口81 n mile處.甲船從A出發,
沿AP方向以9 n mile/h的速度駛向港口,乙船從港口P出發,沿南偏東75°方向,以9 n mile/h的速度駛離港口.現兩船同時出發,
(1)出發后3 h兩船之間的距離是多少?
(2)出發后幾小時乙船在甲船的正東方向?
 |
解:(1)設出發后3h甲船到達C點,乙船到達D點,則PC=54,PD=27.
由題意,可知∠CPD=135°.
在△PCD中,CD2=PC2+PD2-2 PC·PDcos∠CPD ………………………………2分
=542+(27)2-2×54×27×(-)=272×10=7290.
所以CD=27.………………………………………………………………………3分
所以出發后3h兩船相距27 n mile.………………………………………………4分
(2)設出發后xh乙船位于甲船的正東方向,此時甲船到達E點,乙船到達F點,則∠PEF=30°,∠PFE=15°,PE=81-9x,PF=9x.
在△PEF中,=.即=.…………………………7分
解得x=3.……………………………………………………………………………9分
答:出發后3h兩船相距27 n mile,出發后3h乙船在甲船的正東方向.…10分


科目:高中數學 來源: 題型:
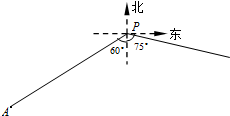 如圖,小島A在港口P的南偏西60°方向,距離港口81n mile處.甲船從A出發,沿AP方向以9n mile/h的速度駛向港口,乙船從港口P出發,沿南偏東75°方向,以9
如圖,小島A在港口P的南偏西60°方向,距離港口81n mile處.甲船從A出發,沿AP方向以9n mile/h的速度駛向港口,乙船從港口P出發,沿南偏東75°方向,以9| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com