
【題目】如圖,四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() .
.
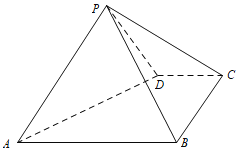
(1)證明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
1)推導出![]() ,從而
,從而![]() ,設
,設![]() 為
為![]() 邊的中點,連結
邊的中點,連結![]() ,
,![]() ,推導出四邊形
,推導出四邊形![]() 為平行四邊形,從而
為平行四邊形,從而![]() ,進而是
,進而是![]() ,
,![]() 面
面![]() ,由此能證明
,由此能證明![]() .
.
(2)推導出面![]() 面
面![]() ,作
,作![]() 于點
于點![]() ,
,![]() 平面
平面![]() ,以
,以![]() 為原點,
為原點,![]() 方向為
方向為![]() 軸,
軸,![]() 方向為
方向為![]() 軸,
軸,![]() 方向為
方向為![]() 軸,建立空間直角坐標系,利用向量法能求出二面角
軸,建立空間直角坐標系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
(1)![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,面
,面![]() 面
面![]() ,
,
![]() ,
,![]()
設![]() 為
為![]() 邊的中點,連結
邊的中點,連結![]() ,
,![]() ,
,
![]() ,
,![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,![]() ,
,
又![]() 為等邊三角形,
為等邊三角形,![]() ,
,
![]() ,
,![]() 面
面![]()
![]() 面
面![]() ,
,
![]() .
.
(2)![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,![]() 面
面![]() 面
面![]() ,
,
在面![]() 中,作
中,作![]() 于點
于點![]() ,
,![]() 平面
平面![]() ,
,
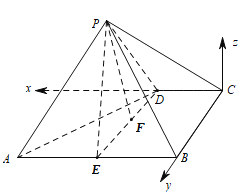
以![]() 為原點,
為原點,![]() 方向為
方向為![]() 軸,
軸,![]() 方向為
方向為![]() 軸,
軸,![]() 方向為
方向為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
如圖所示.則![]() ,2,
,2,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,
設![]() 為平面
為平面![]() 的法向量,則
的法向量,則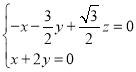 ,
,
取![]() ,得
,得![]() ,
,
![]() 為平面
為平面![]() 的法向量,
的法向量,
則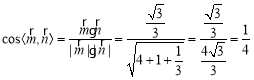 .
.
![]() 二面角
二面角![]() 為銳角,
為銳角,
![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上一點,且
上一點,且![]() .三棱錐
.三棱錐![]() 的各個頂點都在球
的各個頂點都在球![]() 表面上,過點
表面上,過點![]() 作球
作球![]() 的截面,若所得截面圓的面積的最大值與最小值之差為
的截面,若所得截面圓的面積的最大值與最小值之差為![]() ,則球
,則球![]() 的表面積為( )
的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
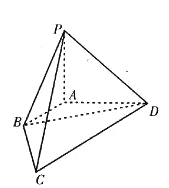
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,且
,且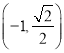 在橢圓E上.
在橢圓E上.
(1)求橢圓E的標準方程;
(2)已知垂直于x軸的直線![]() 交E于A、B兩點,垂直于y軸的直線
交E于A、B兩點,垂直于y軸的直線![]() 交E于C、D兩點,
交E于C、D兩點,![]() 與
與![]() 的交點為P,且
的交點為P,且![]() ,間:是否存在兩定點M,N,使得
,間:是否存在兩定點M,N,使得![]() 為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
為定值?若存在,求出M,N的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《宋人撲棗圖軸》是作于宋朝的中國古畫,現收藏于中國臺北故宮博物院.該作品簡介:院角的棗樹結實累累,小孩群來攀扯,枝椏不停晃動,粒粒棗子搖落滿地,有的牽起衣角,有的捧著盤子拾取,又玩又吃,一片興高采烈之情,躍然于絹素之上.甲、乙、丙、丁四人想根據該圖編排一個舞蹈,舞蹈中他們要模仿該圖中小孩撲棗的爬、扶、撿、頂四個動作,四人每人模仿一個動作.若他們采用抽簽的方式來決定誰模仿哪個動作,則甲不模仿“爬”且乙不模仿“扶”的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點,![]() 軸非負半軸為極軸,長度單位相同,建立極坐標系,曲線
軸非負半軸為極軸,長度單位相同,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() .
.
(1)將曲線![]() 的極坐標方程化為直角坐標方程,寫出直線
的極坐標方程化為直角坐標方程,寫出直線![]() 的參數方程的標準形式;
的參數方程的標準形式;
(2)已知直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的左、右頂點為
的左、右頂點為![]() ,
,![]() ,上、下頂點為
,上、下頂點為![]() ,
,![]() ,記四邊形
,記四邊形![]() 的內切圓為
的內切圓為![]() .
.
(1)求圓![]() 的標準方程;
的標準方程;
(2)已知圓![]() 的一條不與坐標軸平行的切線
的一條不與坐標軸平行的切線![]() 交橢圓
交橢圓![]() 于P,M兩點.
于P,M兩點.
(i)求證:![]() ;
;
(ii)試探究![]() 是否為定值.
是否為定值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上且
上且![]() .
.
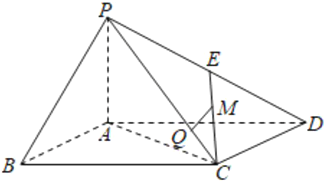
(1)證明![]() 平面
平面![]() ;
;
(2)當![]() 為多大時,在線段
為多大時,在線段![]() 上存在點
上存在點![]() 使得
使得![]() 平面
平面![]() 且
且![]() 與平面
與平面![]() 所成角為
所成角為![]() 同時成立?
同時成立?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com