
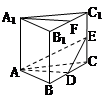
 平面ABC,
平面ABC, CC1⊥AD,從而有AD⊥面B CC1 B1,所以有平面ADE⊥平面BCC1B1;(2)由線面平行的判定定理可知:要證線面平行,只須證明直線與平面內的某一條直線平行即可;不難發現只須證明A1F∥AD,由(1)知AD⊥面B CC1 B1,故只須證明A1F⊥平面BCC1B1,這一點很容易獲得.
CC1⊥AD,從而有AD⊥面B CC1 B1,所以有平面ADE⊥平面BCC1B1;(2)由線面平行的判定定理可知:要證線面平行,只須證明直線與平面內的某一條直線平行即可;不難發現只須證明A1F∥AD,由(1)知AD⊥面B CC1 B1,故只須證明A1F⊥平面BCC1B1,這一點很容易獲得. ABC—A1B1C1是直三棱柱,
ABC—A1B1C1是直三棱柱, CC1⊥面ABC,
CC1⊥面ABC, 平面ABC,
平面ABC, CC1⊥AD
CC1⊥AD AD⊥DE,CC1,DE
AD⊥DE,CC1,DE 平面B CC1B1,CC1∩DE=E
平面B CC1B1,CC1∩DE=E AD⊥面B CC1 B1又AD
AD⊥面B CC1 B1又AD 面ADE
面ADE 平面ADE⊥平面BCC1B1 6分
平面ADE⊥平面BCC1B1 6分 A1B1= A1C1,F為B1C1的中點,
A1B1= A1C1,F為B1C1的中點, AF⊥B1C1
AF⊥B1C1 CC1⊥面A1B1C1且A,F
CC1⊥面A1B1C1且A,F 平面A1B1C1
平面A1B1C1 CC1⊥A、F
CC1⊥A、F 平面BCC1B1,CC1∩B1C1= C1
平面BCC1B1,CC1∩B1C1= C1 A1F⊥平面BCC1B1 由(1)知AD ⊥平面BCC1B1
A1F⊥平面BCC1B1 由(1)知AD ⊥平面BCC1B1 A1F∥AD,又AD
A1F∥AD,又AD 平面ADE,A1F
平面ADE,A1F 平面ADE
平面ADE A1F∥平面ADE 12分
A1F∥平面ADE 12分

科目:高中數學 來源:不詳 題型:解答題
 ,BC=1,AC=CC1=2.
,BC=1,AC=CC1=2. ,求二面角A1-AB-C的大小.
,求二面角A1-AB-C的大小.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 ,N為AB上一點,AB="4AN," M、S分別為PB,BC的中點.以A為原點,射線AB,AC,AP分別為x,y,z軸正向建立如圖空間直角坐標系.
,N為AB上一點,AB="4AN," M、S分別為PB,BC的中點.以A為原點,射線AB,AC,AP分別為x,y,z軸正向建立如圖空間直角坐標系.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 A1N=
A1N= NB1,P為底面正方形A1B1C1D1的中心.求證:MN⊥MC,MP⊥B1C.
NB1,P為底面正方形A1B1C1D1的中心.求證:MN⊥MC,MP⊥B1C.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
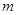 ,
,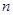 是不重合的兩條直線,
是不重合的兩條直線,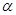 ,
,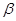 是不重合的兩個平面.下列命題:①若
是不重合的兩個平面.下列命題:①若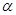 ⊥
⊥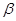 ,
,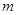 ⊥
⊥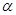 ,則
,則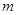 ∥
∥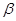 ; ②若
; ②若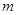 ⊥
⊥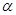 ,
,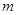 ⊥
⊥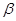 ,則
,則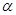 ∥
∥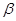 ;③若
;③若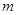 ∥
∥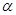 ,
,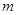 ⊥
⊥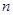 ,則
,則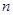 ⊥
⊥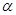 ;④若
;④若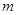 ∥
∥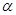 ,
,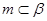 ,則
,則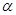 ∥
∥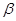 .其中所有真命題的序號是 .
.其中所有真命題的序號是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com