(本小題滿分11分)已知
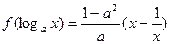
,其中
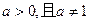
。
(1)求

;
(2)
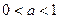
時,判別

的單調性并求
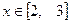
時
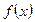
的最小值;
(3)對于

,當
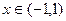
時恒有
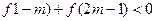
,求
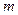
的取值范圍。
(1)
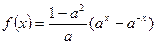
(2)
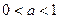
時,

是單調減函數(shù),
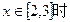

的最大值是
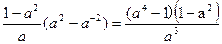
(3)易證
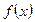
是奇函數(shù),且是增函數(shù),
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
設函數(shù)
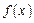
的定義域為
R,當
x<0時,
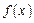
>1,且對任意的實數(shù)
x,
y∈
R,有
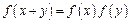
.
(1)求
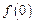
,判斷并證明函數(shù)
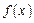
的單調性;
(2)數(shù)列
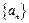
滿足
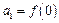
,且
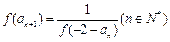
,
①求
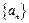
通項公式;
②當
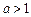
時,不等式
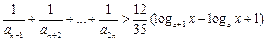
對不小于2的正整數(shù)
恒成立,求
x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
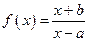
在
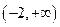
上是增函數(shù)的一個充分非必要條件是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在區(qū)間(1, +∞)上為減函數(shù)的是 ( )
A.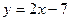 | B.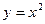 | C.y =" 2" x | D.y = — x 2 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
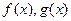
分別是定義在R上的奇函數(shù)和偶函數(shù),當
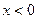
時,
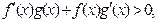
且
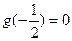
則不等式
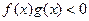
的解集是

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列函數(shù)中,在區(qū)間(0,1)上為減函數(shù)的是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知函數(shù)
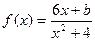
的最大值為
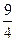
,則實數(shù)
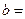
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
定義在
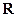
上的函數(shù)
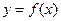
是減函數(shù)且為奇函數(shù),若
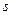
,
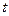
滿足不等式
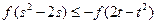
.則當
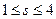
時,

的取值范圍是( )
查看答案和解析>>

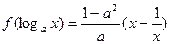 ,其中
,其中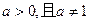 。
。 ;
;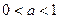 時,判別
時,判別 的單調性并求
的單調性并求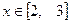 時
時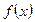 的最小值;
的最小值; ,當
,當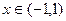 時恒有
時恒有 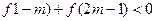 ,求
,求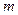 的取值范圍。
的取值范圍。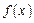 的定義域為R,當x<0時,
的定義域為R,當x<0時,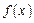 >1,且對任意的實數(shù)x,y∈R,有
>1,且對任意的實數(shù)x,y∈R,有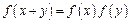 .
.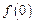 ,判斷并證明函數(shù)
,判斷并證明函數(shù)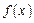 的單調性;
的單調性;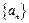 滿足
滿足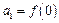 ,且
,且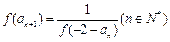 ,
,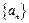 通項公式;
通項公式;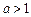 時,不等式
時,不等式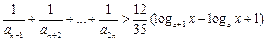 對不小于2的正整數(shù)
對不小于2的正整數(shù)