
解法一:如圖,設點M的坐標為(x,y),
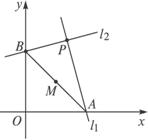
∵M為線段AB的中點,
∴A的坐標為(2x,0),B的坐標為(0,2y).
∵l1⊥l2,且l1、l2過點P(2,4),
∴PA⊥PB,kPA·kPB=-1.而kPA=![]() ,kPB=
,kPB=![]() (x≠1),
(x≠1),
∴![]() =-1(x≠1),整理,得x+2y-5=0(x≠1).
=-1(x≠1),整理,得x+2y-5=0(x≠1).
∵當x=1時,A、B的坐標分別為(2,0)、(0,4),
∴線段AB的中點坐標是(1,2),它滿足方程x+2y-5=0.
綜上所述,點M的軌跡方程是x+2y-5=0.
解法二:如下圖,設M的坐標為(x,y),則A、B兩點的坐標分別是(2x,0)、(0,2y),連結PM.
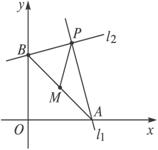
∴l1⊥l2.
∴2|PM|=|AB|.而|PM|=![]() ,
,
|AB|=![]() ,
,
∴2![]() =
=![]() .
.
化簡,得x+2y-5=0,故點M的軌跡方程為x+2y-5=0.


 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:
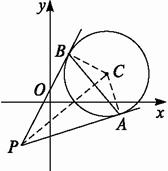
(1)經過圓心C,切點A、B這三點的圓的方程;?
(2)直線AB的方程;?
(3)線段AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com