
【題目】工廠車間某部門有8個小組,在一次技能考試中成績情況分析如下:
小組 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人數 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人數 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
(1)求90分以上人數![]() 對小組序號
對小組序號![]() 的線性回歸方程;
的線性回歸方程;
附:回歸方程為![]() ,其中
,其中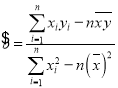 ,
,![]() .本題
.本題![]() ,
,![]() .
.
(2)能否在犯錯誤的概率不超過0.01的前提下認為7組與8組的成績是否優秀(大于90分)與小組有關系.附部分臨界值表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
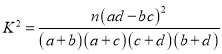 .
.
【答案】(1)![]() (2)能在犯錯誤的概率不超過0.01的前提下不能認為7組與8組的成績是否優秀(大于90分)與小組有關系.
(2)能在犯錯誤的概率不超過0.01的前提下不能認為7組與8組的成績是否優秀(大于90分)與小組有關系.
【解析】
根據題目所給的求線性回歸方程的公式,利用表中內容,求出相對應的![]() ,結合題目所給條件,代入公式,求出相對應的
,結合題目所給條件,代入公式,求出相對應的![]() ,即可求出線性回歸方程。
,即可求出線性回歸方程。
根據題意,列出![]() 列聯表,利用獨立性檢驗的公式,求出
列聯表,利用獨立性檢驗的公式,求出![]() 的值,根據臨界表值,找出對應的概率值,從而得出結論。
的值,根據臨界表值,找出對應的概率值,從而得出結論。
解:(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
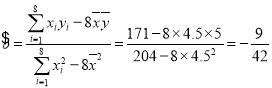 ,
,
![]() ,
,
所以線性回歸方程為![]() .
.
(2)由題意知,![]() 列聯表如下:
列聯表如下:
優秀 | 非優秀 | 合計 | |
7組 | 3 | 42 | 45 |
8組 | 7 | 38 | 45 |
合計 | 10 | 80 | 90 |
![]() ,
,
因為![]() ,所以在犯錯誤的概率不超過0.01的前提下不能認為7組與8組的成績是否優秀(大于90分)與小組有關系.
,所以在犯錯誤的概率不超過0.01的前提下不能認為7組與8組的成績是否優秀(大于90分)與小組有關系.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】某中學調查了某班全部![]() 名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
參加書法社團 | 未參加書法社團 | |
參加演講社團 |
|
|
未參加演講社團 |
|
|
(1)從該班隨機選![]() 名同學,求該同學至少參加上述一個社團的概率;
名同學,求該同學至少參加上述一個社團的概率;
(2)在既參加書法社團又參加演講社團的![]() 名同學中,有5名男同學
名同學中,有5名男同學![]()
![]() 名女同學
名女同學![]() 現從這
現從這![]() 名男同學和
名男同學和![]() 名女同學中各隨機選
名女同學中各隨機選![]() 人,求
人,求![]() 被選中且
被選中且![]() 未被選中的概率.
未被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,其左頂點
,其左頂點![]() 在圓
在圓![]() 上.
上.

(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 為橢圓
為橢圓![]() 上不同于點
上不同于點![]() 的點,直線
的點,直線![]() 與圓
與圓![]() 的另一個交點為
的另一個交點為![]() .是否存在點
.是否存在點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區有1500戶居民,其中平原地區1050戶,山區450戶.為調查該地區2017年家庭收入情況,從而更好地實施“精準扶貧”,采用分層抽樣的方法,收集了150戶家庭2017年年收入的樣本數據(單位:萬元).
(Ⅰ)應收集多少戶山區家庭的樣本數據?
(Ⅱ)根據這150個樣本數據,得到2017年家庭收入的頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果將頻率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
.如果將頻率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
(Ⅲ)樣本數據中,由5戶山區家庭的年收入超過2萬元,請完成2017年家庭收入與地區的列聯表,并判斷是否有![]() 的把握認為“該地區2017年家庭年收入與地區有關”?
的把握認為“該地區2017年家庭年收入與地區有關”?
附:![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸,且兩個坐標系取相等的長度單位,已知直線
軸的正半軸為極軸,且兩個坐標系取相等的長度單位,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),曲線
),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若![]() ,求直線
,求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,當
兩點,當![]() 變化時,求
變化時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程,并求其離心率;
的方程,并求其離心率;
(2)過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,設點
,設點![]() 為第四象限內一點且在橢圓
為第四象限內一點且在橢圓![]() 上(點
上(點![]() 不在直線
不在直線![]() 上),點
上),點![]() 關于
關于![]() 的對稱點為
的對稱點為![]() ,直線
,直線![]() 與
與![]() 交于另一點
交于另一點![]() .設
.設![]() 為原點,判斷直線
為原點,判斷直線![]() 與直線
與直線![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com