
| A. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | B. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | ||
| C. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | D. | [kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$](k∈Z) |
分析 首先通過三角函數(shù)的恒等變換,變換成正弦型函數(shù),進一步利用平移變換,最后根據(jù)正弦型函數(shù)的單調(diào)性求得結(jié)果.
解答 解:f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$)的圖象向左平移φ(0<φ<$\frac{π}{2}$)個單位,得到
g(x)=2sin(2x+2φ-$\frac{π}{6}$).
∵g(x)≤|g($\frac{π}{6}$)|對x∈R恒成立,
∴g($\frac{π}{6}$)=±1,即2sin(2×$\frac{π}{6}$+2φ-$\frac{π}{6}$)=±1,
∴φ=kπ+$\frac{π}{6}$,(k∈Z)
∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,
∴g(x)=2sin(2x+$\frac{π}{6}$).
令2x+$\frac{π}{6}$∈[2kπ+$\frac{π}{2}$,2kπ+π],(k∈Z)
則x∈[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z)
故選:C.
點評 本題考查的知識要點:三角函數(shù)的恒等變換,函數(shù)圖象的平移變換問題,及函數(shù)單調(diào)區(qū)間問題,屬于基礎(chǔ)題型.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $m≤\frac{3}{2}\;,\;\;n=\frac{5}{2}$ | B. | m≤3,n=2 | C. | $m>\frac{3}{2}$ | D. | m>3,n=2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
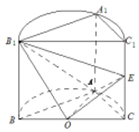 如圖,已知平面BCC1B1是圓柱的軸截面(經(jīng)過圓柱的軸截面)BC是圓柱底面的直徑,O為底面圓心,E為母線CC1的中點,已知AB=AC=AA1=4
如圖,已知平面BCC1B1是圓柱的軸截面(經(jīng)過圓柱的軸截面)BC是圓柱底面的直徑,O為底面圓心,E為母線CC1的中點,已知AB=AC=AA1=4查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com