
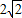 .
.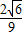 ,若存在,指出點Q的位置,若不存在,說明理由.
,若存在,指出點Q的位置,若不存在,說明理由.
 ,底面ABCD是矩形,我們易求出棱錐VP-BCD的體積,再根據VP-BCD=VC-PBD,我們只要求出△PBD的面積,然后代入棱錐體積公式,即可求出點C到平面PBD的距離.
,底面ABCD是矩形,我們易求出棱錐VP-BCD的體積,再根據VP-BCD=VC-PBD,我們只要求出△PBD的面積,然后代入棱錐體積公式,即可求出點C到平面PBD的距離. 解:(Ⅰ)在Rt△BAD中,AD=2,BD=
解:(Ⅰ)在Rt△BAD中,AD=2,BD= ,
, (2分)
(2分) ,
, ,(4分)
,(4分) (5分)
(5分) ,(6分)
,(6分) ,
,
 .(8分)
.(8分) ,(10分)
,(10分) =
= (12分)
(12分) ,
, ,∵0<λ<1,∴
,∵0<λ<1,∴ (13分)
(13分) (14分)
(14分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
 如圖三棱錐P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=
如圖三棱錐P-ABC中,平面PAB⊥平面ABC,AC⊥BC,BC=| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖三棱錐P-ABC中,△ABC是正三角形,∠PCA=90°,D為PA的中點,二面角P-AC-B為120°,PC=2,AB=2
如圖三棱錐P-ABC中,△ABC是正三角形,∠PCA=90°,D為PA的中點,二面角P-AC-B為120°,PC=2,AB=2| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖三棱錐P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.
如圖三棱錐P-ABC,已知PC⊥平面ABC,CD⊥面PAB,BA=BC,PC=AC=2.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖三棱錐P-ABC中,△PAC,△ABC是等邊三角形.
如圖三棱錐P-ABC中,△PAC,△ABC是等邊三角形.查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com