
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
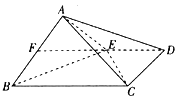
(Ⅰ)證明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)見解析;
(II)![]()
【解析】
(Ⅰ)取BC的中點G,連接FG,EG,證明四邊形EGCD為平行四邊形,得EG∥平面ACD,再證明FG∥平面ACD,可得平面EFG∥平面ACD,從而得到EF∥平面ACD;
(Ⅱ)求解三角形證明BA⊥AE,取BE的中點H,連接AH,HC,證明AH⊥平面BCDE.以H為坐標原點,以過點H且平行于CD的直線為x軸,以過點H且平行于BC的直線為y軸,HA所在直線為z軸建立空間直角坐標系,求出平面ACD的一個法向量,再求出直線BC的方向向量,由兩向量所成角的余弦值可得直線BC與平面ACD所成角的正弦值.
解:證明:(I)作![]() 中點
中點![]() ,連接
,連接![]() ,則
,則![]() ,
,
又![]() ,
,![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,
故![]() ,則
,則![]() 平面
平面![]() ,
,
又![]()
![]() 為
為![]() 的中點,
的中點,![]() ,則
,則![]() 平面
平面![]() ,
,
又![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
(II)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,則
,則![]() ,
,
又![]() ,
,![]() ,則
,則![]() ,
,
作![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,
,![]() 平面
平面![]() .
.
以![]() 為坐標原點,以過點
為坐標原點,以過點![]() 且平行于
且平行于![]() 的直線為
的直線為![]() 軸,以過點
軸,以過點![]() 且平行于
且平行于![]() 的直線為
的直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立如圖所示的空間直角坐標系,
軸,建立如圖所示的空間直角坐標系,

可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
設(shè)![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
則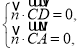 即
即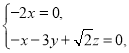
可得![]() ,
,
直線![]() 的方向向量
的方向向量![]() ,
,
設(shè)![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
則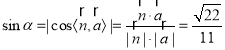 ,
,
綜上,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】如圖,圓臺O1O2的軸截面為等腰梯形A1A2B2B1,A1A2![]() B1B2,A1A2=2B1B2,A1B1=2,圓臺O1O2的側(cè)面積為6π.若點C,D分別為圓O1,O2上的動點且點C,D在平面A1A2B2B1的同側(cè).
B1B2,A1A2=2B1B2,A1B1=2,圓臺O1O2的側(cè)面積為6π.若點C,D分別為圓O1,O2上的動點且點C,D在平面A1A2B2B1的同側(cè).
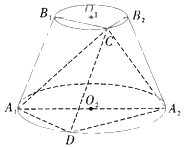
(1)求證:A1C⊥A2C;
(2)若∠B1B2C=60°,則當三棱錐C﹣A1DA2的體積取最大值時,求A1D與平面CA1A2所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】端午節(jié)(每年農(nóng)歷五月初五),是中國傳統(tǒng)節(jié)日,有吃粽子的習俗.某超市在端午節(jié)這一天,每售出![]() kg粽子獲利潤
kg粽子獲利潤![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg虧損
kg虧損![]() 元.根據(jù)歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節(jié)預購進了
元.根據(jù)歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節(jié)預購進了![]() kg粽子.以
kg粽子.以![]() (單位:kg,
(單位:kg,![]() )表示今年的市場需求量,
)表示今年的市場需求量,![]() (單位:元)表示今年的利潤.
(單位:元)表示今年的利潤.
市場需求量(kg) |
|
|
|
|
|
頻率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)根據(jù)頻率分布表估計今年利潤![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于空間中的三條直線,有以下四個條件:①三條直線兩兩相交;②三條直線兩兩平行;③三條直線共點;④兩直線相交,第三條平行于其中一條與另一條相交.其中使這三條直線共面的充分條件有______(填正確結(jié)論的序號).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
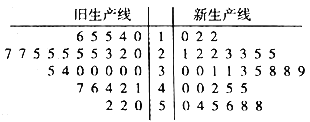
【題目】近幾年,我國鮮切花產(chǎn)業(yè)得到了快速發(fā)展,相關(guān)部門制定了鮮切花產(chǎn)品行業(yè)等級標準,統(tǒng)一使用綜合指標值![]() 進行衡量,如下表所示.某花卉生產(chǎn)基地準備購進一套新型的生產(chǎn)線,現(xiàn)進行設(shè)備試用,分別從新舊兩條生產(chǎn)線加工的產(chǎn)品中選取30個樣品進行等級評定,整理成如圖所示的莖葉圖.
進行衡量,如下表所示.某花卉生產(chǎn)基地準備購進一套新型的生產(chǎn)線,現(xiàn)進行設(shè)備試用,分別從新舊兩條生產(chǎn)線加工的產(chǎn)品中選取30個樣品進行等級評定,整理成如圖所示的莖葉圖.
綜合指標 |
|
|
|
質(zhì)量等級 | 三級 | 二級 | 一級 |
(Ⅰ)根據(jù)莖葉圖比較兩條生產(chǎn)線加工的產(chǎn)品的綜合指標值的平均值及分散程度(直接給出結(jié)論即可);
(Ⅱ)若從等級為三級的樣品中隨機選取3個進行生產(chǎn)流程調(diào)查,其中來自新型生產(chǎn)線的樣品個數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根據(jù)該花卉生產(chǎn)基地的生產(chǎn)記錄,原有生產(chǎn)線加工的產(chǎn)品的單件平均利潤為4元,產(chǎn)品的銷售率(某等級產(chǎn)品的銷量與產(chǎn)量的比值)及產(chǎn)品售價如下表:
三級花 | 二級花 | 一級花 | |
銷售率 |
|
|
|
單件售價 | 12元 | 16元 | 20元 |
預計該新型生產(chǎn)線加工的鮮切花單件產(chǎn)品的成本為10元,日產(chǎn)量3000件.因為鮮切花產(chǎn)品的保鮮特點,未售出的產(chǎn)品統(tǒng)一按原售價的50%全部處理完.如果僅從單件產(chǎn)品利潤的角度考慮,該生產(chǎn)基地是否需要引進該新型生產(chǎn)線?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“金鑲玉”是北京奧運會的獎牌設(shè)計所采用的式樣,喻示中國傳統(tǒng)文化中的“金玉良緣”,體現(xiàn)了中國人對奧林匹克精神的禮贊和對運動員的褒獎.它的設(shè)計方案,創(chuàng)意十分新穎,突破了以往任何一屆奧運會獎牌設(shè)計單一材質(zhì)的傳統(tǒng),又融入了典型的中國文化元素,是中國文化與體育精神完美結(jié)合的載體.現(xiàn)有一矩形玉片![]() ,
,![]() 為
為![]() 毫米,
毫米,![]() 為32毫米,
為32毫米,![]() 為
為![]() 的中點.現(xiàn)要開槽鑲嵌金絲,將其加工為鑲金工藝品,如圖,金絲部分為優(yōu)弧
的中點.現(xiàn)要開槽鑲嵌金絲,將其加工為鑲金工藝品,如圖,金絲部分為優(yōu)弧![]() 和線段
和線段![]() 其中優(yōu)弧
其中優(yōu)弧![]() 所在圓的圓心為
所在圓的圓心為![]() ,圓
,圓![]() 與矩形的邊
與矩形的邊![]() 分別相切于點
分別相切于點![]() 以及點
以及點![]() 在線段
在線段![]() 上(
上(![]() 在
在![]() 的左側(cè)),
的左側(cè)),![]() 分別于圓
分別于圓![]() 相切于點
相切于點![]() 且
且![]() .若優(yōu)弧
.若優(yōu)弧![]() 部分鑲嵌的金絲每毫米造價為
部分鑲嵌的金絲每毫米造價為![]() 元(
元(![]() ),線段
),線段![]() 部分鑲嵌的金絲每毫米造價為
部分鑲嵌的金絲每毫米造價為![]() 元.記銳角
元.記銳角![]() 鑲嵌金絲的總造價為
鑲嵌金絲的總造價為![]() 元.
元.
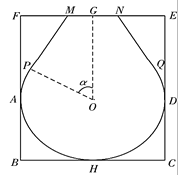
(1)試表示出關(guān)于![]() 的函數(shù)
的函數(shù)![]() 并寫出
并寫出![]() 的范圍;
的范圍;
(2)當鑲嵌金絲的總造價最低時,求出四邊形![]() 的面積
的面積![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知對數(shù)函數(shù)![]() 過定點
過定點![]() (其中
(其中![]() ),函數(shù)
),函數(shù)![]() (其中
(其中![]() 為
為![]() 的導函數(shù),
的導函數(shù),![]() ,
,![]() 為常數(shù))
為常數(shù))
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)若對![]() 有
有![]() 恒成立,且
恒成立,且![]() 在
在![]() (
(![]() )處的導數(shù)相等,求證:
)處的導數(shù)相等,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 與拋物線
與拋物線![]() 有共同的焦點,且離心率為
有共同的焦點,且離心率為![]() ,設(shè)
,設(shè)![]() 分別是
分別是![]() 為橢圓的上下頂點
為橢圓的上下頂點
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 與
與![]() 軸不垂直的直線
軸不垂直的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,當弦
,當弦![]() 的中點
的中點![]() 落在四邊形
落在四邊形![]() 內(nèi)(含邊界)時,求直線
內(nèi)(含邊界)時,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com